题目内容
20．
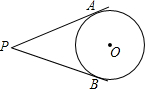PA，PB分别切⊙O于A，B两点，点C为⊙O上不同于AB的任意一点，已知∠P=40°，则∠ACB的度数是70°或110°．
分析 连接OA、OB，可求得∠AOB，再分点C在$\widehat{AB}$上和$\widehat{ABC}$上，可求得答案．
解答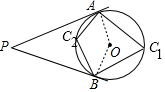 
解：
如图，连接OA、OB，
∵PA，PB分别切⊙O于A，B两点，
∴∠PAO=∠PBO=90°，
∴∠AOB=360°-90°-90°-40°=140°，
当点C1在$\widehat{ABC}$上时，则∠AC1B=$\frac{1}{2}$∠AOB=70°，
当点C2在$\widehat{AB}$上时，则∠AC2B+∠AC1B=180°，
∴∠AC2B=110°，
故答案为：70°或110°．
点评 本题主要考查切线的性质，由条件求得∠AOB是解题的关键，注意分点C在优弧和劣弧上两种情况．
练习册系列答案
相关题目
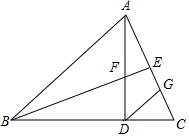如图，在△ABC中，AB=BC，AD⊥BC于点D，点E为AC中点，连接BE交AD于点F，且BF=AC，过点D作DG∥AB，交AC于点G．
8．下列表述中，能确定准确位置的是（ ）
| A． | 教室第三排 | B． | 湖心南路 | ||
| C． | 南偏东40° | D． | 东经112°，北纬51° |
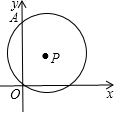如图，点P（1，2），⊙P经过原点O，交y轴正半轴于点A，点B在⊙P上，∠BAO=45°，则点B的坐标是（3，1）或（-1，3）．