题目内容
 已知,M是等边△ABC边BC上的点.
已知,M是等边△ABC边BC上的点.(1)如图1,过点M作MN∥AC且交于点N,求证:BM=BN;
(2)如图2,连接AM,过点M作∠AMH=60°,MH与∠ACB的邻补角的平分线交与点H,过H作HD⊥BC于点D.求证:MA=MH.
分析:(1)由条件可以得出∠A=∠B=∠C=60°,再根据平行线的性质就可以得出∠BMN=∠BNM=60°,得出△BNM是等边三角形就可以得出结论;
(2)过点M作MN∥AC交AB于N,由条件可以得出∠HMC=∠BAM,∠ANM=∠MCH和AN=BC就可以得出△ANM≌△MCH,就可以得出结论.
(2)过点M作MN∥AC交AB于N,由条件可以得出∠HMC=∠BAM,∠ANM=∠MCH和AN=BC就可以得出△ANM≌△MCH,就可以得出结论.
解答:解:(1)∵△ABC是等边三角形,
∴∠A=∠B=∠C=60°,AB=BC=AC.
∵MN∥AC,
∴∠BMN=∠C=60°,∠BNM=∠A=60°.
∴∠BMN=∠BNM=∠B=60°,
∴△BNM是等边三角形,
∴BM=BN;
(2)过点M作MN∥AC交AB于N,
∴BM=BN,∠ANM=120°.
∵∠AMH=60°,
∴∠AMB+∠HMC=120°.
∵∠B=60°,
∴∠AMB+∠BAM=120°.
∴∠HMC=∠BAM.
∵∠ACB=60°,
∴∠ACD=120°.
∵CH平分∠ACD,
∴∠ACH=
∠ACD=60°,
∴∠MCH=120°,
∴∠ANM=∠MCH.
∵AB=BC,
∴AB-BN=BC-BM,
∴AN=BC.
在△ANM和△MCH中,
,
∴△ANM≌△MCH(ASA),
∴MA=MH.
∴∠A=∠B=∠C=60°,AB=BC=AC.
∵MN∥AC,
∴∠BMN=∠C=60°,∠BNM=∠A=60°.

∴∠BMN=∠BNM=∠B=60°,
∴△BNM是等边三角形,
∴BM=BN;
(2)过点M作MN∥AC交AB于N,
∴BM=BN,∠ANM=120°.
∵∠AMH=60°,
∴∠AMB+∠HMC=120°.
∵∠B=60°,
∴∠AMB+∠BAM=120°.
∴∠HMC=∠BAM.
∵∠ACB=60°,
∴∠ACD=120°.
∵CH平分∠ACD,
∴∠ACH=
| 1 |
| 2 |
∴∠MCH=120°,
∴∠ANM=∠MCH.
∵AB=BC,
∴AB-BN=BC-BM,
∴AN=BC.
在△ANM和△MCH中,
|
∴△ANM≌△MCH(ASA),
∴MA=MH.
点评:本题考查了等边三角形的性质的运用,平行线的性质的运用,角平分线的性质的运用,全等时间性的判定与性质的运用,解答时证明三角形全等是关键.

练习册系列答案
相关题目
 明理由;你能发现四边形APDQ的面积与△ABC的面积有何关系吗?为什么?
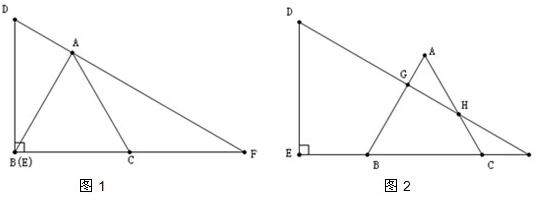
明理由;你能发现四边形APDQ的面积与△ABC的面积有何关系吗?为什么? 19、已知,△ABC是等边三角形,将一块含30°角的直角三角板DEF如图放置,让三角板在BC所在的直线l上向右平移.当点E与点B重合时,点A恰好落在三角板的斜边DF上.
19、已知,△ABC是等边三角形,将一块含30°角的直角三角板DEF如图放置,让三角板在BC所在的直线l上向右平移.当点E与点B重合时,点A恰好落在三角板的斜边DF上.