题目内容
22、已知,△ABC是等边三角形,将一块含有30°角的直角三角板DEF如图放置,让三角板在BC所在的直线上向右平移,如图1,当点E与点B重合时,点A恰好落在三角形的斜边DF上.
(1)利用图1证明:EF=2BC;
(2)在三角板的平移过程中,在图2中线段EB=AH是否始终成立(假定AB,AC与三角板斜边的交点为G、H)?如果成立,请证明;如果不成立,请说明理由?
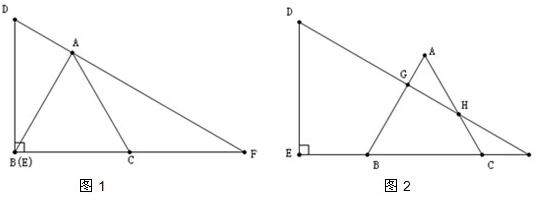
(1)利用图1证明:EF=2BC;
(2)在三角板的平移过程中,在图2中线段EB=AH是否始终成立(假定AB,AC与三角板斜边的交点为G、H)?如果成立,请证明;如果不成立,请说明理由?

分析:(1)根据等边三角形的性质,得∠ACB=60°,AC=BC.结合三角形外角的性质,得∠CAF=60°-30°=30°,则CF=AC,从而证明结论;
(2)根据(1)中的证明方法,得到CH=CF.根据(1)中的结论,知BE+CF=AC,从而证明结论.
(2)根据(1)中的证明方法,得到CH=CF.根据(1)中的结论,知BE+CF=AC,从而证明结论.
解答:解:(1)∵△ABC是等边三角形,
∴∠ACB=60°,AC=BC.
∵∠F=30°
∴∠CAF=60°-30°=30°.
∴∠CAF=∠F,
∴CF=AC,
∴CF=AC=EC,
∴EF=2BC.(4分)
(2)成立. (1分)
根据(1)中证CF=AC的方法,同理,得CH=CF.
∵EF=2BC,
∴BE+CF=BC.
又∵AH+CH=AC,AC=BC,
∴AH=BE.(9分)
∴∠ACB=60°,AC=BC.
∵∠F=30°
∴∠CAF=60°-30°=30°.
∴∠CAF=∠F,
∴CF=AC,
∴CF=AC=EC,
∴EF=2BC.(4分)
(2)成立. (1分)
根据(1)中证CF=AC的方法,同理,得CH=CF.
∵EF=2BC,
∴BE+CF=BC.
又∵AH+CH=AC,AC=BC,
∴AH=BE.(9分)
点评:此题综合运用了等边三角形的性质、三角形的外角性质以及等腰三角形的判定及性质.

练习册系列答案
相关题目
某“研究性学习小组”遇到了以下问题,请参与:
已知,△ABC是等边三角形且内接于⊙O,取
上异于A、B的点M.设直线CA与BM相交于点K,直线CB与AM相交于点N.
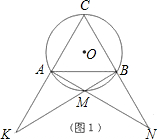

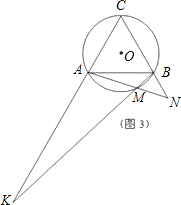
(1)如图1,图2,图3,M分别为
的中点、三分之一点、四分之一点,△ABC的边长均为2,分别测量出AK、BN的长,计算AK•BN的值(精确到0.01)并将结果填入下表中:
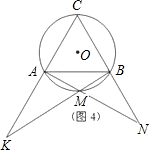
(2)如图4,当M为
上任意一点时,根据(1)的结果,猜想AK•BN与AB的数量关系式为 ;
(3)对(2)中提出的猜想,依图4给出证明.
已知,△ABC是等边三角形且内接于⊙O,取
 |
| AB |




(1)如图1,图2,图3,M分别为
 |
| AB |
| △ABC的边长 | AK•BN的值 | |
| 图1 | 2 | |
| 图2 | 2 | |
| 图3 | 2 |
 |
| AB |
(3)对(2)中提出的猜想,依图4给出证明.
 三个为条件,余下的一个为结论,组成一个正确的命题(只需写出一种),并给予证明.
三个为条件,余下的一个为结论,组成一个正确的命题(只需写出一种),并给予证明.
