题目内容
如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与x轴相交于点A(-3,0),与y轴交于点B,且与正比例函数y=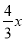 的图象交点为C(m,4)求:
的图象交点为C(m,4)求:
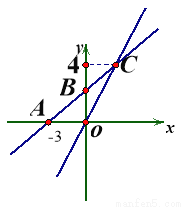
(1)一次函数y=kx+b的解析式;
(2)若点D在第二象限,△DAB是以AB为直角边的等腰直角三角形,直接写出点D的坐标。
(3)在x轴上求一点P使△POC为等腰三角形,请直接写出所有符合条件的点P的坐标.
(1) ;(2) (-2,5)或(-5,3).(3) (5,0)或(-5,0)或(6,0)或(,0). 【解析】 试题分析:(1)首先利用待定系数法把C(m,4)代入正比例函数y=中,计算出m的值,进而得到C点坐标,再利用待定系数法把A、C两点坐标代入一次函数y=kx+b中,计算出k、b的值,进而得到一次函数解析式. (2)利用△BED1≌△AOB,△BED2≌△AOB,即可得出...
练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目

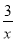 的图象上,若x1<0<x2<x3, 则下列式子正确的是( )
的图象上,若x1<0<x2<x3, 则下列式子正确的是( )
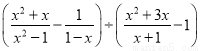 ,其中x=2.
,其中x=2.