题目内容
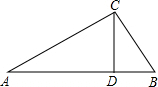 响水县为迎接省卫生文明城市建设,我校把一块形状为直角三角形的废地开辟为植物园,如图所示,∠ACB=90°,AC=80m,BC=60m,若线段CD是一条水渠,且点D在边AB上,已知水渠的造价为100元/米,问点D在距点A多远处时,水渠的造价最低?最低造价是多少?
响水县为迎接省卫生文明城市建设,我校把一块形状为直角三角形的废地开辟为植物园,如图所示,∠ACB=90°,AC=80m,BC=60m,若线段CD是一条水渠,且点D在边AB上,已知水渠的造价为100元/米,问点D在距点A多远处时,水渠的造价最低?最低造价是多少?考点:勾股定理的应用
专题:
分析:当CD为斜边上的高时,CD最短,从而水渠造价最低,根据已知条件可将CD的长求出,在Rt△ACD中运用勾股定理可将AD边求出.
解答:解:当CD为斜边上的高时,CD最短,从而水渠造价最低,
∵∠ACB=90°,AC=80米,BC=60米,
∴AB=
=
=100米,
∵CD•AB=AC•BC,即CD•100=80×60,
∴CD=48米,
∴在Rt△ACD中AC=80,CD=48,
∴AD=
=
=64米,
48×100=4800(元).
综上所述,D点在距A点64米的地方,水渠的造价最低,其最低造价为4800元.
∵∠ACB=90°,AC=80米,BC=60米,
∴AB=
| AC2+BC2 |
| 602+802 |
∵CD•AB=AC•BC,即CD•100=80×60,
∴CD=48米,
∴在Rt△ACD中AC=80,CD=48,
∴AD=
| AC2-CD2 |
| 802-482 |
48×100=4800(元).
综上所述,D点在距A点64米的地方,水渠的造价最低,其最低造价为4800元.
点评:本题考查了勾股定理的应用.解题的关键是确定D点的位置,在运算过程中多次用到勾股定理.

练习册系列答案
相关题目
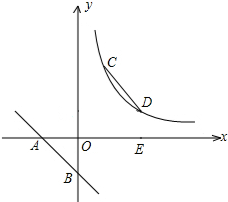 已知直线y=-2x-2交坐标轴于A,B两点,E为y轴上一点,线段AB沿AE方向平移到CD,反比例函数y=
已知直线y=-2x-2交坐标轴于A,B两点,E为y轴上一点,线段AB沿AE方向平移到CD,反比例函数y=