题目内容
（2013•娄底）如图，将直角三角板60°角的顶点放在圆心O上，斜边和一直角边分别与⊙O相交于A、B两点，P是优弧AB上任意一点（与A、B不重合），则∠APB=30°
30°
．分析：根据在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半，即可得出答案．
解答：解：由题意得，∠AOB=60°，
则∠APB=
∠AOB=30°．
故答案为：30°．
则∠APB=
| 1 |
| 2 |
故答案为：30°．
点评：本题考查了圆周角定理的知识，解答本题的关键是熟练掌握圆周角定理的内容．
练习册系列答案
开心练习课课练与单元检测系列答案
相关题目
（2013•娄底）如图，⊙O1，⊙O2、相交于A、B两点，两圆半径分别为6cm和8cm，两圆的连心线O1O2的长为10cm，则弦AB的长为（ ）
（2013•娄底）如图，已知A点是反比例函数
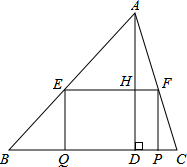（2013•娄底）如图，在△ABC中，∠B=45°，BC=5，高AD=4，矩形EFPQ的一边QP在BC边上，E、F分别在AB、AC上，AD交EF于点H．