题目内容
（2013•娄底）如图，⊙O1，⊙O2、相交于A、B两点，两圆半径分别为6cm和8cm，两圆的连心线O1O2的长为10cm，则弦AB的长为（ ）分析：根据相交两圆的性质得出AC=
AB，进而利用勾股定理得出AC的长．
| 1 |
| 2 |
解答：解：连接AO1，AO2，
∵⊙O1，⊙O2相交于A、B两点，两圆半径分别为6cm和8cm，两圆的连心线O1O2的长为10cm，
∴O1O2⊥AB，
∴AC=
AB，
设O1C=x，则O2C=10-x，
∴62-x2=82-（10-x）2，
解得：x=3.6，
∴AC2=62-x2=36-3.62=23.04，
∴AC=4.8cm，
∴弦AB的长为：9.6cm．
故选B．
∵⊙O1，⊙O2相交于A、B两点，两圆半径分别为6cm和8cm，两圆的连心线O1O2的长为10cm，
∴O1O2⊥AB，
∴AC=
| 1 |
| 2 |
设O1C=x，则O2C=10-x，
∴62-x2=82-（10-x）2，
解得：x=3.6，
∴AC2=62-x2=36-3.62=23.04，
∴AC=4.8cm，
∴弦AB的长为：9.6cm．
故选B．
点评：此题考查了相交圆的性质与勾股定理．此题难度适中，注意掌握辅助线的作法，注意数形结合思想与方程思想的应用．
练习册系列答案
一线名师提优试卷系列答案
相关题目
（2013•娄底）如图，已知A点是反比例函数
（2013•娄底）如图，将直角三角板60°角的顶点放在圆心O上，斜边和一直角边分别与⊙O相交于A、B两点，P是优弧AB上任意一点（与A、B不重合），则∠APB=
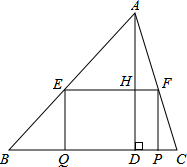（2013•娄底）如图，在△ABC中，∠B=45°，BC=5，高AD=4，矩形EFPQ的一边QP在BC边上，E、F分别在AB、AC上，AD交EF于点H．