题目内容
10．在Rt△ABC中，∠C=90°，AB=$\sqrt{6}$，BC=$\sqrt{3}$，求∠A的度数．分析 根据三角函数定义可计算出sinA=$\frac{CB}{AB}$=$\frac{\sqrt{3}}{\sqrt{6}}$=$\sqrt{\frac{1}{2}}$=$\frac{\sqrt{2}}{2}$，再根据特殊角的三角函数数值可得答案．
解答 
解：∵∠C=90°，AB=$\sqrt{6}$，BC=$\sqrt{3}$，
∴sinA=$\frac{CB}{AB}$=$\frac{\sqrt{3}}{\sqrt{6}}$=$\sqrt{\frac{1}{2}}$=$\frac{\sqrt{2}}{2}$，
∴∠A=45°．
点评 此题主要考查了解直角三角形，关键是掌握三角函数的定义，以及特殊角的三角函数值．
练习册系列答案
相关题目
1．为鼓励大学生创业，我市为在开发区创业的每位大学生提供无息贷款125000元，这个数据用科学记数法表示为（保留两位有效数字）（ ）
| A． | 1.2×105 | B． | 1.2×105 | C． | 1.3×105 | D． | 1.3×106 |
15．下列运算中，计算结果正确的是（ ）
| A． | 3x-2x=1 | B． | x•x=x2 | C． | 2x+2x=2x2 | D． | （-a3）2=a5 |
2．
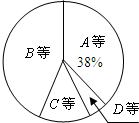某校为了解九年级男生1000米长跑的成绩，从中随机抽取了50名男生进行测试，根据测试评分标准，将他们的得分进行统计后分为A，B，C，D四等，并绘制成下面的频数分布表和扇形统计图．
（1）试直接写出x、y的值；
（2）求表示得分为C等的扇形的圆心角的度数；
（3）如果该校九年级共有男生200名，试估计这200名男生中成绩达到A等和B等的人数共有多少人？
某校为了解九年级男生1000米长跑的成绩，从中随机抽取了50名男生进行测试，根据测试评分标准，将他们的得分进行统计后分为A，B，C，D四等，并绘制成下面的频数分布表和扇形统计图．| 等第 | 成绩（得分） | 频数（人数） | 频率 |
| A | 10分 | 7 | 0.14 |
| 9分 | x | 0.24 | |
| B | 8分 | 15 | 0.30 |
| 7分 | 8 | 0.16 | |
| C | 6分 | 4 | 0.08 |
| 5分 | 1 | y | |
| D | 5分以下 | 3 | 0.06 |
| 合计 | 50 | 1.00 |
（2）求表示得分为C等的扇形的圆心角的度数；
（3）如果该校九年级共有男生200名，试估计这200名男生中成绩达到A等和B等的人数共有多少人？