Question

9．如图，AC是⊙O的直径，PB切⊙O于点D，交AC的延长线于点B，且∠DAB=∠B．
（1）求∠B的度数；
（2）若BD=9，求BC的长．

Answer 1

分析 （1）连结OD，根据切线的性质得出OD⊥PB，再由圆周角定理得出∠COD=2∠DAB，根据∠DAB=∠B，可知∠COD=2∠B，再由直角三角形的性质即可得出结论；
（2）在Rt△BOD中，根据锐角三角函数的定义得出OD及OB的长，进而可得出结论．

解答 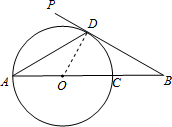解：（1）连结OD，
∵PB切⊙O于点D，
∴OD⊥PB
∵∠COD=2∠DAB，∠DAB=∠B，
∴∠COD=2∠B，
∴在Rt△BOD中，∠B=30°；

（2）在Rt△BOD中，
∵BD=9，∠B=30°，
∴OD=OC=3$\sqrt{3}$，OB=6$\sqrt{3}$，
∴BC=3$\sqrt{3}$．

点评 本题考查的是切线的性质，根据题意作出辅助线，构造出直角三角形是解答此题的关键．