题目内容
18. 已知抛物线y=ax2+bx+2过点A(-1,-1),B(1,3).
已知抛物线y=ax2+bx+2过点A(-1,-1),B(1,3).(1)求此抛物线的函数解析式;
(2)该抛物线的对称轴是x=1,顶点坐标是(1,3);
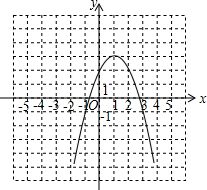
(3)选取适当的数据填入下表,并在直角坐标系内描点画出该抛物线的图象.
| x | … | … | |||||
| y | … | … |
分析 (1)将A与B坐标代入二次函数解析式求出a与c的值,即可确定出二次函数解析式;
(2)化成顶点式确定出对称轴,以及顶点坐标,
(3)根据5点法画出图象即可.
解答 解:(1)∵抛物线y=ax2+bx+2过点A(-1,-1),B(1,3).
∴$\left\{\begin{array}{l}{a-b+2=-1}\\{a+b+2=3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-1}\\{b=2}\end{array}\right.$,
则二次函数解析式为y=-x2+2x+2;
(2)∵y=-x2+2x+2=-(x-1)2+3,
∴对称轴为直线x=1,顶点坐标为(1,3),
(3)列表:
| x | … | -1 | 0 | 1 | 2 | 3 | … |
| y | … | -1 | 2 | 3 | 2 | -1 | … |
点评 此题考查了待定系数法求二次函数解析式、二次函数的图象,以及二次函数的性质,熟练掌握待定系数法是解本题的关键.

练习册系列答案
 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
6.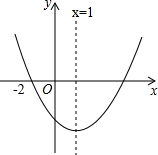 二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中:①abc<0;②2a+b=0;③当-2<x<3,y<0;④当x>1时,y随x的增大而减小,正确的个数是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中:①abc<0;②2a+b=0;③当-2<x<3,y<0;④当x>1时,y随x的增大而减小,正确的个数是( )
 二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中:①abc<0;②2a+b=0;③当-2<x<3,y<0;④当x>1时,y随x的增大而减小,正确的个数是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中:①abc<0;②2a+b=0;③当-2<x<3,y<0;④当x>1时,y随x的增大而减小,正确的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
7.点A在点O的南偏东30°,点B在点O的北偏西70°,则OA,OB这两条射线构成的角等于( )
| A. | 140° | B. | 100° | C. | 80° | D. | 40° |
8.一元二次方程(x+1)2=4的根是( )
| A. | x1=2,x2=-2 | B. | x=-3 | C. | x1=1,x2=-3 | D. | x=1 |
 已知一次函数y1=2x-3与y2=-x+4的图象相交于点P,它们与y轴交于A、B两点.
已知一次函数y1=2x-3与y2=-x+4的图象相交于点P,它们与y轴交于A、B两点. 如图,在斜坡的顶部有一铁塔AB,B是CD的中点,CD是水平的,在阳光的照射下,塔影DE留在坡面上.已知CD=12m,DE=18m,小明和小华的身高都是1.5m,同一时刻小明站在E处,影子落在坡面上,影长为2m,小华站在平地上,影子也落在平地上,影长为1m,则塔高AB是22.5米.
如图,在斜坡的顶部有一铁塔AB,B是CD的中点,CD是水平的,在阳光的照射下,塔影DE留在坡面上.已知CD=12m,DE=18m,小明和小华的身高都是1.5m,同一时刻小明站在E处,影子落在坡面上,影长为2m,小华站在平地上,影子也落在平地上,影长为1m,则塔高AB是22.5米. 如图,在正方形ABCD中,E为BC边上的点(不与B,C重合),F为CD边上的点(不与C,D重合),且AE=AF,AB=4,设△AEF的面积为y,EC的长为x,求y关于x的函数关系式,并写出自变量x的取值范围.
如图,在正方形ABCD中,E为BC边上的点(不与B,C重合),F为CD边上的点(不与C,D重合),且AE=AF,AB=4,设△AEF的面积为y,EC的长为x,求y关于x的函数关系式,并写出自变量x的取值范围.