Question

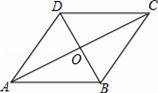
如图，在▱ABCD中，对角线AC与BD相交于点O，∠CAB=∠ACB．

（1）求证：四边形ABCD为菱形；

（2）若AB=12，∠DAB=60°，求四边形ABCD的面积．

Answer 1

【考点】菱形的判定与性质；平行四边形的性质．

【分析】（1）根据等腰三角形的判定得出AB=BC，根据菱形的判定得出即可；

（2）根据菱形的性质得出AO=OC，BO=OD，AC⊥ND，求出AO、OD，求出AC和BD，根据面积公式求出即可．

【解答】证明：（1）∵∠CAB=∠ACB，

∴AB=BC，

∵四边形ABCD是平行四边形，

∴四边形ABCD为菱形；

 

（2）∵四边形ABCD为菱形，

∴AC⊥BD，

又∵∠DAB=60°，

∴∠OAB=∠DAB=30°

在Rt△AOB中，

OB=AB=×12=6，

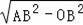
∴OA===6，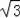

∴BD=20B=12，AC=20A=12，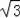

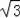
∴S_菱形ABCD=BD×AC=×12×12=72．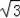

【点评】本题考查了勾股定理，菱形的性质和判定的应用，能熟记菱形的性质和判定定理是解此题的关键．