Question

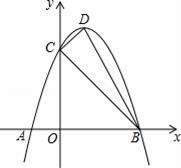
如图，已知抛物线y=ax²+bx+3交x轴于A、B两点（A在B左边），交y轴于C点，且OC=3OA，对称轴x=1交抛物线于D点．

（1）求抛物线解析式；

（2）求证：△BCD为直角三角形；

（3）在x轴上方的抛物线上，是否存在点M，过M作MN⊥x轴于N点，使△BMN与△BCD相似？若存在，请求出M的坐标；若不存在，请说明理由．

Answer 1

【考点】二次函数综合题．

【分析】（1）将x=0代入可求得y=3，故此可知C（0，3），OC=3，OA=1，则点A的坐标为（﹣1，0），由点B与点A关于x=1对称可知B（3，0），将点A、点B的坐标代入抛物线的解析式，从而求得a=﹣1，b=2；

（2）先利用配方法求出抛物线的顶点D的坐标，再利用两点间的距离公式得出CD²+BC²=BD²，由勾股定理的逆定理即可证明△BCD为直角三角形；

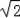
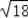
（3）由（2）知，CD=，BC==3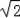．设M（x，﹣x²+2x+3），则MN=﹣x²+2x+3，BN=3﹣x，由于∠MNB=∠BCD=90°，所以当△BMN与△BCD相似时，分两种情况：①△BMN∽△BDC；②△BMN∽△DBC．然后根据相似三角形的性质列出关于x的方程，从而求得点M的坐标．

【解答】解：（1）∵将x=0代入y=ax²+bx+3，得y=3，

∴C（0，3）．

∵OC=3OA，

∴OA=1，

∴A（﹣1，0）．

∵点B与点A关于x=1对称，

∴B（3，0）．

将A（﹣1，0），B（3，0）代入y=ax²+bx+3得：

，

解得：．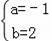

∴抛物线解析式为y=﹣x²+2x+3；

 

（2）∵y=﹣x²+2x+3=﹣（x﹣1）²+4，

∴顶点D的坐标为（1，4）．

∵A（﹣1，0），B（3，0），C（0，3），

∴CD²=（1﹣0）²+（4﹣3）²=2，

 BC²=（3﹣0）²+（0﹣3）²=18，

BD²=（1﹣3）²+（4﹣0）²=20，

∴CD²+BC²=BD²，

∴△BCD为直角三角形；

 

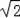
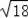
（3）由（2）知，CD=，BC==3．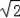

设在x轴上方的抛物线上存在点M（x，﹣x²+2x+3），则﹣1＜x＜3，﹣x²+2x+3＞0，

∵MN⊥x轴于N点，

∴N（x，0），∠MNB=90°，

∴BN=3﹣x，MN=﹣x²+2x+3．

∵Rt△BCD中，∠BCD=90°，

∴∠MNB=∠BCD=90°，

∴当△BMN与△BCD相似时，分两种情况：

①如果△BMN∽△BDC，那么=，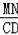

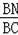
即=，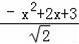

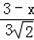
解得x₁=3，x₂=﹣，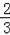

又∵﹣1＜x＜3，

∴x=﹣，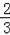

∴﹣x²+2x+3=，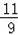

∴M（﹣，）；

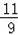
②如果△BMN∽△DBC，那么=，

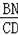
即=，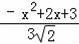

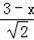
解得x₁=2，x₂=3，

又∵﹣1＜x＜3，

∴x=2，

∴﹣x²+2x+3=3，

∴M（2，3）．

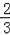
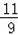
综上所述，M点坐标为（﹣，）或（2，3）．

【点评】本题是二次函数综合题，其中涉及到利用待定系数法求二次函数的解析式、二次函数的性质、两点间的距离公式、勾股定理的逆定理、相似三角形的性质等知识点，利用分类讨论、数形结合与方程思想是解题的关键．