题目内容
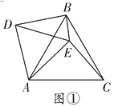
【题目】已知:如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() .
.![]() 是边
是边![]() 的中点,点
的中点,点![]() 为边
为边![]() 上的一个动点(与点
上的一个动点(与点![]() 、
、![]() 不重合),过点
不重合),过点![]() 作
作![]() ,交边
,交边![]() 于点
于点![]() .联结
.联结![]() 、
、![]() ,设
,设![]() .
.
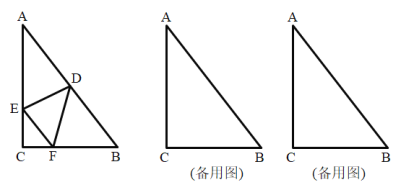
(1)当![]() 时,求
时,求![]() 的面积;
的面积;
(2)如果点![]() 关于
关于![]() 的对称点为
的对称点为![]() ,点
,点![]() 恰好落在边
恰好落在边![]() 上时,求
上时,求![]() 的值;
的值;
(3)以点![]() 为圆心,
为圆心,![]() 长为半径的圆与以点
长为半径的圆与以点![]() 为圆心,
为圆心,![]() 长为半径的圆相交,另一个交点
长为半径的圆相交,另一个交点![]() 恰好落在线段
恰好落在线段![]() 上,求
上,求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根据题意过E作EM⊥AB于M,根据勾股定理和三角函数定义以及由平行线分线段成比例定理可得EF的长,根据三角形面积公式即可得出结论;
(2)根据题意过E作EN⊥AB于N,连接DD',交EF于Q,由对称进行分析并根据三角函数计算以及证明四边形ENDQ是矩形,进而得出则![]() ,最后利用三角函数即可得出结论;
,最后利用三角函数即可得出结论;
(3)根据题意设![]() 与
与![]() 相交于点
相交于点![]() ,并计算AF的长,根据平行线分线段成比例定理可得AG的长,证明
,并计算AF的长,根据平行线分线段成比例定理可得AG的长,证明![]() ,得
,得![]() ,列方程解出即可.
,列方程解出即可.
解:(1)过点![]() 作
作![]() ,垂足为点
,垂足为点![]() .
.
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() .
.
∵![]() ,
,![]() ,
,
∴![]() .
.
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
又∵![]() ,
,
∴![]() .
.
∴![]() .
.
(2)过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,设
,设![]() 与
与![]() 相交于点
相交于点![]() .
.
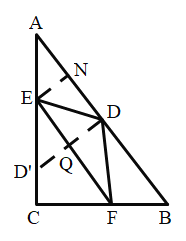
∵![]() 、
、![]() 关于
关于![]() 对称,
对称,
∴![]() ,
,![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() .
.
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
∴![]() .
.
∴![]() .
.
∵![]() ,
,![]() ,
,![]() ,
,
∴∠END=∠NDQ=∠EQD=90°,
∴四边形ENDQ是矩形,
∴![]() .
.
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() .
.
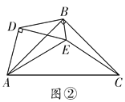
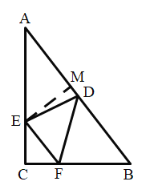
(3)设![]() 与
与![]() 相交于点
相交于点![]() ,如下图,
,如下图,
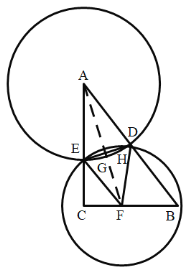
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]() .
.
∴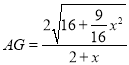 .
.
∵圆![]() 和圆
和圆![]() 相交,
相交,
∴![]() .
.
∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]() .
.
∴![]() .
.
∴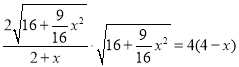 .
.
解得![]() (舍去),
(舍去),![]() .
.

 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案【题目】小云在学习过程中遇到一个函数![]() .下面是小云对其探究的过程,请补充完整:
.下面是小云对其探究的过程,请补充完整:
(1)当![]() 时,对于函数
时,对于函数![]() ,即
,即![]() ,当
,当![]() 时,
时,![]() 随
随![]() 的增大而 ,且
的增大而 ,且![]() ;对于函数
;对于函数![]() ,当
,当![]() 时,
时,![]() 随
随![]() 的增大而 ,且
的增大而 ,且![]() ;结合上述分析,进一步探究发现,对于函数
;结合上述分析,进一步探究发现,对于函数![]() ,当
,当![]() 时,
时,![]() 随
随![]() 的增大而 .
的增大而 .
(2)当![]() 时,对于函数
时,对于函数![]() ,当
,当![]() 时,
时,![]() 与
与![]() 的几组对应值如下表:
的几组对应值如下表:
| 0 |
| 1 |
| 2 |
| 3 |
|
| 0 |
|
|
| 1 |
|
|
|
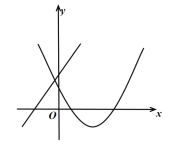
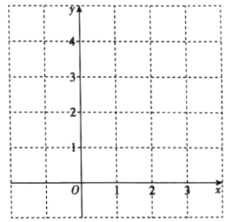
综合上表,进一步探究发现,当![]() 时,
时,![]() 随
随![]() 的增大而增大.在平面直角坐标系
的增大而增大.在平面直角坐标系![]() 中,画出当
中,画出当![]() 时的函数
时的函数![]() 的图象.
的图象.
(3)过点(0,m)(![]() )作平行于
)作平行于![]() 轴的直线
轴的直线![]() ,结合(1)(2)的分析,解决问题:若直线
,结合(1)(2)的分析,解决问题:若直线![]() 与函数
与函数![]() 的图象有两个交点,则
的图象有两个交点,则![]() 的最大值是 .
的最大值是 .