题目内容
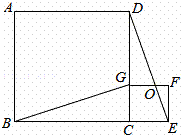
如图,四边形ABCD、CEFG都是正方形,点G在线段CD上,连接BG、DE,DE和FG相交于点O,设AB=a,CG=b(a>b).下列结论:①△BCG≌△DCE;②BG⊥DE;③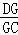 =
=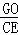 ;④(a﹣b)2•S△EFO=b2•S△DGO.其中结论正确的个数是( )
;④(a﹣b)2•S△EFO=b2•S△DGO.其中结论正确的个数是( )
A. 4个 B.3个 C.2个 D. 1个
B 证明:①∵四边形ABCD和四边形CEFG是正方形,
∴BC=DC,CG=CE,∠BCD=∠ECG=90°,
∴∠BCG=∠DCE,
在△BCG和△DCE中,
 ,
,
∴△BCG≌△DCE(SAS),
故①正确;
②延长BG交DE于点H,
∵△BCG≌△DCE,
∴∠CBG=∠CDE,
又∵∠CBG+∠BGC=90°,
∴∠CDE+∠DGH=90°,
∴∠DHG=90°,
∴BH⊥DE;
∴BG⊥DE.
故②正确;
③∵四边形GCEF是正方形,
∴GF∥CE,
∴ =
=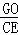 ,
,
∴ =
= 是错误的.
是错误的.
故③错误;
④∵DC∥EF,
∴∠GDO=∠OEF,
∵∠GOD=∠FOE,
∴△OGD∽△OFE,
∴ =(
=( )2=(
)2=( )2=
)2= ,
,
∴(a﹣b)2•S△EFO=b2•S△DGO.
故④正确;
.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目




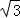 ,点P在⊙O上,当∠OPA最大时,PA的长等于( )
,点P在⊙O上,当∠OPA最大时,PA的长等于( )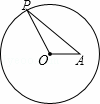
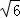 C3 D. 2
C3 D. 2