题目内容
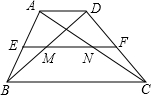如图，梯形ABCD的中位线EF分别交对角线BD、AC于点M，N，AD=1，BC=3，则EF=________，MN=________．
2 1
分析：由梯形ABCD的中位线EF分别交对角线BD、AC于点M，N，根据梯形的中位线定理即可求解；
解答：∵梯形ABCD的中位线EF分别交对角线BD、AC于点M，N，
∴EM=
AD，NF=AD，EF=（AD+BC），
∵AD=1，BC=3，∴EM=，NF=，EF=2，
∴MN=EF-EM-NF=2--=1，
故答案为：2，1．
点评：本题考查了梯形中位线定理，属于基础题，关键是正确运用梯形的中位线定理．
分析：由梯形ABCD的中位线EF分别交对角线BD、AC于点M，N，根据梯形的中位线定理即可求解；
解答：∵梯形ABCD的中位线EF分别交对角线BD、AC于点M，N，
∴EM=
AD，NF=AD，EF=（AD+BC），∵AD=1，BC=3，∴EM=
，NF=，EF=2，∴MN=EF-EM-NF=2-
-=1，故答案为：2，1．
点评：本题考查了梯形中位线定理，属于基础题，关键是正确运用梯形的中位线定理．
练习册系列答案
相关题目
如图，梯形ABCD的对角线交于点O，有以下四个结论：①△AOB∽△COD，②△AOD∽△ACB，③S△DOC：S△AOD=DC：AB，④S△AOD=S△BOC，其中始终正确的有（ ）个．
| A、1 | B、2 | C、3 | D、4 |
14、如图，梯形ABCD的两条对角线交于点E，图中面积相等的三角形共有
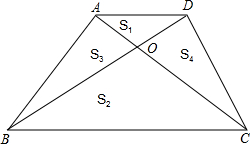如图，梯形ABCD的对角线AC、BD相交于点O，△ADO的面积记作S1，△BCO的面积记作S2，△ABO的面积记作S3，△CDO的面积记作S4，则下列关系正确是（ ）| A、S1=S2 | B、S1×S2=S3×S4 | C、S1+S2=S4+S3 | D、S2=2S3 |
16、如图，梯形ABCD的对角线交于点O，有以下三个结论：
如图，梯形ABCD的面积为34cm2，AE=BF，CE与DF相交于O，△OCD的面积为11cm2，则阴影部分的面积为