题目内容
18.不等式组$\left\{\begin{array}{l}{2x-5≤3(x-1)}\\{\frac{x+7}{2}>4x}\end{array}\right.$的解集是-2≤x<1.分析 先求出不等式的解集,再根据找不等式组解集的规律找出即可.
解答 解:$\left\{\begin{array}{l}{2x-5≤3(x-1)①}\\{\frac{x+7}{2}>4x②}\end{array}\right.$
∵解不等式①得:x≥-2,
解不等式②得:x<1
∴不等式组的解集为-2≤x<1,
故答案为:-2≤x<1.
点评 本题考查了解一元一次不等式和解一元一次不等式组的应用,解此题的关键是能根据不等式的解集找出不等式组的解集,难度适中.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.2015的倒数是( )
| A. | -2015 | B. | $\frac{1}{2015}$ | C. | 2015 | D. | -$\frac{1}{2015}$ |
3.二次根式$\sqrt{(x+3)^{2}}$中字母x的取值范围是( )
| A. | x≠-3 | B. | x≥-3 | C. | x>-3 | D. | 全体实数 |
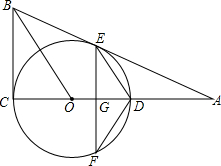 如图,⊙O的圆心在Rt△ABC的直角边AC上,⊙O经过C、D两点,与斜边AB交于点E,连结BO、ED,有BO∥ED,作弦EF⊥AC于G,连结DF.
如图,⊙O的圆心在Rt△ABC的直角边AC上,⊙O经过C、D两点,与斜边AB交于点E,连结BO、ED,有BO∥ED,作弦EF⊥AC于G,连结DF. 如图,BD平分∠ABC,DE∥BC,若∠2=62°,则∠1=31°.
如图,BD平分∠ABC,DE∥BC,若∠2=62°,则∠1=31°. 尺规作图,已知半圆如图,请以直径为底,半径为腰上的高作等腰三角形(不写作法,保留痕迹).
尺规作图,已知半圆如图,请以直径为底,半径为腰上的高作等腰三角形(不写作法,保留痕迹).