题目内容
3.已知两个单项式-2a2bm+1与na2b4的和为0,则m+n的值是5.分析 由题意可知-2a2bm+1与na2b4是同类项,然后由同类项的定义可知m+1=4,由它们的和为0可知n=2.
解答 解:∵单项式-2a2bm+1与na2b4的和为0,
∴m+1=4,n=2.
解得:m=3.
∴m+n=5.
故答案为:5.
点评 本题主要考查的是合并同类项,根据题意求得m、n的值是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.若∠AOB=45°,∠BOC=30°,则∠AOC的度数是( )
| A. | 15° | B. | 30° | C. | 75° | D. | 15°或75° |
11.化简(-x)3•(-x)2的结果正确的是( )
| A. | -x6 | B. | x6 | C. | -x5 | D. | x5 |
18.下列各式变形中,是因式分解的是( )
| A. | a2-2ab+b2-1=(a-b)2-1 | B. | 2x2$+2x=2{x}^{2}(1+\frac{1}{x})$ | ||
| C. | (x+2)(x-2)=x2-4 | D. | x2-6x+9=(x-3)2 |
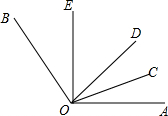 如图所示,OC是∠AOD的平分线,OE是∠BOD的平分线.
如图所示,OC是∠AOD的平分线,OE是∠BOD的平分线.