题目内容
已知关于x的一元二次方程(m-1)x2-2mx+m+2=0,
(1)有两个不相等的实数根,求m的取值范围.
(2)有两个互为相反数的实数根,求m的值,并求此两根.
(1)有两个不相等的实数根,求m的取值范围.
(2)有两个互为相反数的实数根,求m的值,并求此两根.
考点:根的判别式,根与系数的关系
专题:
分析:(1)根据方程有两个不相等的实数根,得出△>0,列出关于m的不等式,求出m的取值范围;
(2)根据根与系数的关系和已知条件得出
=0且m-1≠0,-4m+8≥0,再求解即可.
(2)根据根与系数的关系和已知条件得出
| 2m |
| m-1 |
解答:解:(1)△=(-2m)2-4(m-1)(m+2)=4m2-4m2-4m+8=-4m+8,
根据题意得:-4m+8>0 且m-1≠0,
解得:m<2且m≠1;
(2)根据题意得:
=0且m-1≠0,-4m+8≥0,
则m=0,
当m=0 时,原方程化为x2=2,
解得:x1=
,x2=-
.
根据题意得:-4m+8>0 且m-1≠0,
解得:m<2且m≠1;
(2)根据题意得:
| 2m |
| m-1 |
则m=0,
当m=0 时,原方程化为x2=2,
解得:x1=
| 2 |
| 2 |
点评:本题综合考查了根的判别式和根与系数的关系,在解不等式时一定要注意数值的正负与不等号的变化关系.

练习册系列答案
相关题目
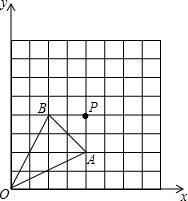 △OAB在坐标系中的位置如图所示.
△OAB在坐标系中的位置如图所示.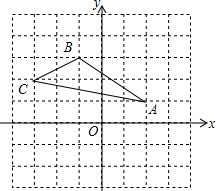 如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(2,1),B(-1,3),C(-3,2).
如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(2,1),B(-1,3),C(-3,2).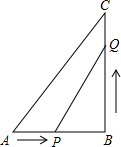 在△ABC中,∠B=90°,AB=6cm,BC=7cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,设P、Q分别从A、B同时出发,运动时间为t秒.
在△ABC中,∠B=90°,AB=6cm,BC=7cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,设P、Q分别从A、B同时出发,运动时间为t秒.