题目内容
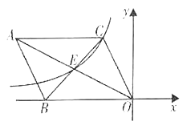
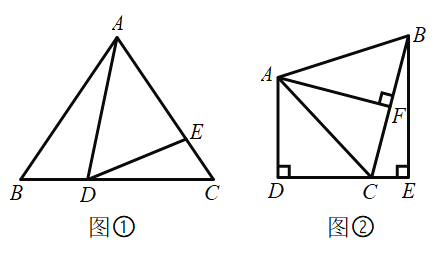
【题目】如图①,在![]() 中,
中,![]() ,点
,点![]() ,
,![]() 分别是边
分别是边![]() ,
,![]() 上的点,且
上的点,且![]() .
.
(1)若![]() ,
,![]() ,设
,设![]() ,
,![]() ,求
,求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)如图②,![]() ,
,![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,点
,点![]() 在线段
在线段![]() 上,
上,![]() ,
,![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)先证明△ABD∽△DCE,进而可得ABCE=BDCD,由此可得![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)先利用等腰三角形的三线合一证得AF⊥BC,BF =5,再利用勾股定理计算即可求得答案.
(1)证明:∵AB=AC,
∴∠B=∠C.
∵∠ADC为△ABD的外角,
∴∠ADC=∠ADE+∠EDC=∠B+∠DAB.
∵∠ADE=∠B,
∴∠BAD=∠CDE.
又∠B=∠C,
∴△ABD∽△DCE.
∴![]() ,
,
∴ABCE=BDCD,
则5×(5-y)=x(6-x),
整理,得![]() .
.
(2)解:∵AB=AC,AF⊥BC,
∴BF=CF=![]() BC=5.
BC=5.
∴在Rt△ACF中,AC=![]() .
.
∴在Rt△ACD中,DC=![]() .
.
在Rt△BCE中,CE=![]() .
.
∴DE=DC+CE=![]() .
.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目