题目内容
7.某花圃用花盆培育某仲花苗,经过试验发现,每盆的盈利与每盆种植的株数构成一定的关系.每盆植入3株时,平均单株盈利3元.以同样的栽培条件,若每盆增加1株,平均单株盈利就减少0.5元,要使每盆盈利达到最大,则每盆应植4株.分析 假设每盆花苗增加x株,则每盆花苗有(x+3)株,得出平均单株盈利为(3-0.5x)元,根据总利润=平均单株盈利×每盆株数,列出函数表达式,根据二次函数性质求解.
解答 解:设每盆花苗增加x株,每盆利润为W,则每盆花苗有(x+3)株,平均单株盈利为:(3-0.5x)元,
W=(x+3)(3-0.5x)
=-$\frac{1}{2}$x2+$\frac{3}{2}$x+9
=-$\frac{1}{2}$(x-$\frac{3}{2}$)2+10$\frac{1}{8}$
∵x为正整数,
∴x=1或2时,每盆盈利达到最大,
根据实际,每盆应植4株,每盆盈利达到最大.
故答案为:4.
点评 此题考查了二次函数的应用,根据每盆花苗株数×平均单株盈利=总盈利得出二次函数表达式是解题关键,特别注意x是整数.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
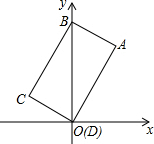 如图,把矩形ABCD按如图所示方式放置,若点A的坐标为(2,3),点B的坐标为(0,4).
如图,把矩形ABCD按如图所示方式放置,若点A的坐标为(2,3),点B的坐标为(0,4).