题目内容
在△ABC中,AB=AC,P是BC上任意一点.
(1)如图①,若P是BC边上任意一点,PF⊥AB于点F,PE⊥AC于点E,BD为△ABC的高线,试探求PE,PF与BD之间的数量关系;
(2)如图②,若P是BC延长线上一点,PF⊥AB于点F,PE⊥AC于点E,CD为△ABC的高线,试探求PE,PF与CD之间的数量关系.

(1)如图①,若P是BC边上任意一点,PF⊥AB于点F,PE⊥AC于点E,BD为△ABC的高线,试探求PE,PF与BD之间的数量关系;
(2)如图②,若P是BC延长线上一点,PF⊥AB于点F,PE⊥AC于点E,CD为△ABC的高线,试探求PE,PF与CD之间的数量关系.

考点:等腰三角形的性质
专题:
分析:(1)连接AP,根据S△ABC=S△ABP+S△ACP列式整理即可得解;
(2)连接AP,根据S△ABC=S△ABP-S△ACP列式整理即可得解.
(2)连接AP,根据S△ABC=S△ABP-S△ACP列式整理即可得解.
解答: 解:(1)如图,连接AP,则S△ABC=S△ABP+S△ACP,
解:(1)如图,连接AP,则S△ABC=S△ABP+S△ACP,
所以,
AC•BD=
AB•PF+
AC•PE,
∵AB=AC,
∴BD=PE+PF;
(2)连接AP,则S△ABC=S△ABP-S△ACP,
所以,
AB•CD=
AB•PF-
AC•PE,
∵AB=AC,
∴CD=PF-PE.
 解:(1)如图,连接AP,则S△ABC=S△ABP+S△ACP,
解:(1)如图,连接AP,则S△ABC=S△ABP+S△ACP,所以,
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵AB=AC,
∴BD=PE+PF;
(2)连接AP,则S△ABC=S△ABP-S△ACP,
所以,
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵AB=AC,
∴CD=PF-PE.
点评:本题考查了等腰三角形的性质,利用三角形的面积列出等式是解题的关键.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
在下面四个说法中正确的有( )
①互为相反数的两个数的绝对值相等 ②正数的绝对值等于它本身
③一个数的倒数等于它本身,这个数是±1 ④没有最大的整数
⑤几个有理数相乘,如果负因数有奇数个,则积为负数.
①互为相反数的两个数的绝对值相等 ②正数的绝对值等于它本身
③一个数的倒数等于它本身,这个数是±1 ④没有最大的整数
⑤几个有理数相乘,如果负因数有奇数个,则积为负数.
| A、1个 | B、2个 | C、3个 | D、4个 |
已知凸四边形ABCD中,∠A=∠C=90°.
(1)如图①,若DE平分∠ADC,BF平分∠ABC的邻补角,求证:DE⊥BF;
(2)如图②,若BF、DE分别平分∠ABC、∠ADC的邻补角,判断DE∥BF.

(1)如图①,若DE平分∠ADC,BF平分∠ABC的邻补角,求证:DE⊥BF;
(2)如图②,若BF、DE分别平分∠ABC、∠ADC的邻补角,判断DE∥BF.

若ab≠0,则
+
的值不可能是( )
| a |
| |a| |
| |b| |
| b |
| A、2 | B、0 | C、-2 | D、1 |
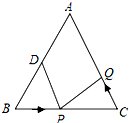 如图,已知△ABC中,AB=AC=20cm,∠ABC=∠ACB,BC=16cm,点D是AB的中点.点P在线段BC上以6厘米/秒的速度由B点向C点运动,同时点Q在线段CA上由C点向A点运动,且点Q的运动速度与点P的运动速度相等.经过1秒后,△BPD与△CQP是否全等,请说明理由.
如图,已知△ABC中,AB=AC=20cm,∠ABC=∠ACB,BC=16cm,点D是AB的中点.点P在线段BC上以6厘米/秒的速度由B点向C点运动,同时点Q在线段CA上由C点向A点运动,且点Q的运动速度与点P的运动速度相等.经过1秒后,△BPD与△CQP是否全等,请说明理由. 如图,已知AD平分∠BAC,AB=AC,则此图中全等三角形有
如图,已知AD平分∠BAC,AB=AC,则此图中全等三角形有