题目内容
 如图所示,在等腰梯形ABCD中,已知AD∥BC,AB=DC,∠ACB=42°,∠ACD=27°.
如图所示,在等腰梯形ABCD中,已知AD∥BC,AB=DC,∠ACB=42°,∠ACD=27°.(1)∠BAC=
69
69
°;(2)如果BC=10cm,连接BD,求BD的长度.
分析:(1)先求出∠BCD的度数,根据等腰梯形的性质可得出∠ABC的度数,在△ABC中利用勾股定理可得出∠BAC的度数;
(2)结合(1)的结论,可得出AC=BC,再由等腰梯形的对角线相等即可得出BD的长度.
(2)结合(1)的结论,可得出AC=BC,再由等腰梯形的对角线相等即可得出BD的长度.
解答:解:(1)∵∠ACB=42°,∠ACD=27°,
∴∠BCD=∠BCA+∠ACD=69°;
(2)∵∠ABC=∠BAC=69°,
∴AC=BC=10cm,
又∵四边形ABCD是等腰梯形,
∴BD=AC=10cm.
∴∠BCD=∠BCA+∠ACD=69°;
(2)∵∠ABC=∠BAC=69°,
∴AC=BC=10cm,
又∵四边形ABCD是等腰梯形,
∴BD=AC=10cm.
点评:本题考查了等腰梯形的性质,解答本题关键是掌握等腰梯形的对角线相等,同一底边上的底角相等.

练习册系列答案
 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
 25、如图所示,在等腰梯形ABCD中,AD∥BC,AB=CD,点P为BC边上任意一点,且
25、如图所示,在等腰梯形ABCD中,AD∥BC,AB=CD,点P为BC边上任意一点,且 1、如图所示,在等腰梯形ABCD中,AD∥BC,DE⊥BC于点E,BF⊥AE于点F,请你添加一个条件,使△ABF≌△CDE.
1、如图所示,在等腰梯形ABCD中,AD∥BC,DE⊥BC于点E,BF⊥AE于点F,请你添加一个条件,使△ABF≌△CDE. 48、如图所示,在等腰梯形ABCD中,AD∥BC,AB=CD,DE⊥BC于E,BF⊥AE于F,AE=BE.请你判断线段BF与图形中哪条线段相等,先写出你的猜想,再加以证明.
48、如图所示,在等腰梯形ABCD中,AD∥BC,AB=CD,DE⊥BC于E,BF⊥AE于F,AE=BE.请你判断线段BF与图形中哪条线段相等,先写出你的猜想,再加以证明.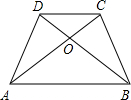 如图所示,在等腰梯形ABCD中,AB∥CD,若AB+CD=4,并且∠AOB=120°,则该等腰梯形的面积为
如图所示,在等腰梯形ABCD中,AB∥CD,若AB+CD=4,并且∠AOB=120°,则该等腰梯形的面积为 如图所示,在等腰梯形ABCD中,AD∥BC,过A作腰CD的平行线,AE∥CD,AB=AD=DC,∠B=60°
如图所示,在等腰梯形ABCD中,AD∥BC,过A作腰CD的平行线,AE∥CD,AB=AD=DC,∠B=60°