Question

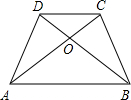如图所示，在等腰梯形ABCD中，AB∥CD，若AB+CD=4，并且∠AOB=120°，则该等腰梯形的面积为

 

（结果保留根号的形式）．

Answer 1

分析：过点C作对角线BD的平行线CE交AB的延长线于点E，则可得到△ACE是等腰三角形，根据等腰梯形的性质可证得△ADC≌△BCE，则等腰梯形的面积转化为求△ACE的面积．

解答：解：过点C作对角线BD的平行线CE交AB的延长线于点E，
∵∠AOB=120度，△ACE是等腰三角形，且底边AE=4，∴∠CAB=30°，
过C作高CF，则CF=

3

3

×2=

2 3

3

．
则△ACE的面积是

4 3

3

．
而△ACE的面积等于梯形ABCD的面积．因而等腰梯形的面积为

4

3

3

．

点评：此题考查等腰梯形的性质及梯形中常见的辅助线的作法，通过这条辅助线可以把两对角线的夹角的问题转化为三角形的角的问题．