题目内容
已知正三角形的边长为6，则这个正三角形的外接圆半径是________．
2
分析：过圆心作一边的垂线，根据勾股定理可以计算出外接圆半径．
解答：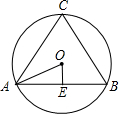
解：如图所示，△ABC是正三角形，故O是△ABC的中心，
∵正三角形的边长为6，
∴AE=
×6=3，OE=AE•tan30°=3×
=，
∴AO=
=
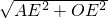=2．
故答案为：2．
点评：考查了三角形外接圆以及利用勾股定理简单计算的能力．
分析：过圆心作一边的垂线，根据勾股定理可以计算出外接圆半径．
解答：
解：如图所示，△ABC是正三角形，故O是△ABC的中心，∵正三角形的边长为6，
∴AE=
×6=3，OE=AE•tan30°=3×=，∴AO=
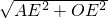==2．故答案为：2
．点评：考查了三角形外接圆以及利用勾股定理简单计算的能力．
练习册系列答案
阅读快车系列答案
相关题目
已知正三角形的边长为6，则其内切圆的半径为（ ）
A、2
| ||
| B、3 | ||
C、
| ||
| D、1 |
已知正三角形的边长为6，则这个正三角形的外接圆半径是（ ）
A、
| ||
B、2
| ||
| C、3 | ||
D、3
|
已知正三角形的边长为3，则它的外接圆的面积为（ ）
| A、3π | ||||
| B、6π | ||||
| C、9π | ||||
D、
|
如图，“凸轮”的外围由以正三角形的顶点为圆心，以正三角形的边长为半径的三段等弧组成．已知正三角形的边长为1，则凸轮的周长等于（ ）