题目内容
如图，甲、乙两船同时从港口O出发，甲船以16.1海里/时的速度向东偏南32°方向航行，乙船向西偏南58°方向航行，航行了两小时，甲船到达A处并观测到B处的乙船恰好在其正西方向．（1）求甲船从港口O到A处的航行距离；
（2）求乙船的速度V（精确到0.1海里/时）．
【答案】分析：本题可以求出船行进的距离OA，根据三角函数就可以求出OB，就可以求出乙船的速度．
解答：
解：
（1）由题可知：OA=16.1×2=32.2．
（2）∠A=32°，∠B=58°，
则在Rt△OCA中，sinA=
°．
∴OC=OA•sin32°≈17.06（海里）．
在Rt△OBC中，sinB=
=sin58°，
∴OB=
（海里）．
∴V乙=
（海里/时）．
答：求甲船从港口O到A处的航行距离是32.2海里；求乙船的速度V约是10.1海里/时．
点评：本题主要考查三角函数的定义，理解方向角的定义是解决本题的关键．
解答：
解：（1）由题可知：OA=16.1×2=32.2．
（2）∠A=32°，∠B=58°，
则在Rt△OCA中，sinA=
°．∴OC=OA•sin32°≈17.06（海里）．
在Rt△OBC中，sinB=
=sin58°，∴OB=
（海里）．∴V乙=
（海里/时）．答：求甲船从港口O到A处的航行距离是32.2海里；求乙船的速度V约是10.1海里/时．
点评：本题主要考查三角函数的定义，理解方向角的定义是解决本题的关键．
练习册系列答案
相关题目
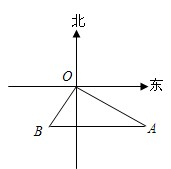，乙船向西偏南58°方向航行，航行了两小时，甲船到达A处并观测到B处的乙船恰好在其正西方向．
6、如图，甲、乙两船同时从港口O出发，其中甲船沿北偏西30°方向航行，乙船沿南偏西70°方向航行，已知两船的航行速度相同，如果1小时后甲、乙两船分别到达点A、B处，那么点B位于点A的（ ）
