题目内容
【题目】在平面直角坐标系![]() 中,已知抛物线
中,已知抛物线![]() .
.
(1)求抛物线的对称轴;
(2)当![]() 时,设抛物线与
时,设抛物线与![]() 轴交于
轴交于![]() 两点(点
两点(点![]() 在点
在点![]() 左侧),顶点为
左侧),顶点为![]() ,若
,若![]() 为等边三角形,求
为等边三角形,求![]() 的值;
的值;
(3)过![]() (其中
(其中![]() )且垂直
)且垂直![]() 轴的直线
轴的直线![]() 与抛物线交于
与抛物线交于![]() 两点.若对于满足条件的任意
两点.若对于满足条件的任意![]() 值,线段
值,线段![]() 的长都不小于1,结合函数图象,直接写出
的长都不小于1,结合函数图象,直接写出![]() 的取值范围.
的取值范围.
【答案】(1)x=2;(2)![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】
(1)利用配方法将二次函数解析式变形为顶点式,由此即可得出抛物线的对称轴;
(2)利用二次函数图象上点的坐标特征可得出点A,B的坐标,由(1)可得出顶点C的坐标,再利用等边三角形的性质可得出关于a的一元一次方程,解之即可得出a值;
(3)分![]() 及
及![]() 两种情况考虑:①当
两种情况考虑:①当![]() 时,利用二次函数图象上点的坐标特征可得出关于a的一元一次不等式,解之即可得出a的取值范围;②当
时,利用二次函数图象上点的坐标特征可得出关于a的一元一次不等式,解之即可得出a的取值范围;②当![]() 时,利用二次函数图象上点的坐标特征可得出关于a的一元一次不等式,解之即可得出a的取值范围.综上,此题得解.
时,利用二次函数图象上点的坐标特征可得出关于a的一元一次不等式,解之即可得出a的取值范围.综上,此题得解.
(1)∵![]() ,
,
∴抛物线的对称轴为直线![]() .
.
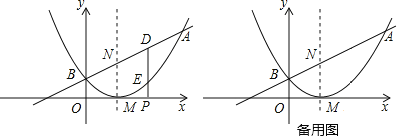
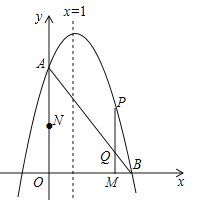
(2)依照题意,画出图形,如图1所示.
当![]() 时,
时,![]() ,即
,即![]() ,
,
解得:![]() ,
,![]() .
.
由(1)可知,顶点![]() 的坐标为
的坐标为![]() .
.
∵![]() ,
,
∴![]() .
.
∵![]() 为等边三角形,
为等边三角形,
∴点![]() 的坐标为
的坐标为![]() ,
,
∴![]() ,
,
∴![]() .
.
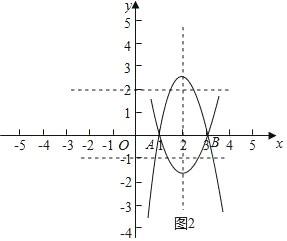
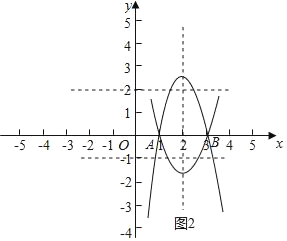
(3)分两种情况考虑,如图2所示:
①当![]() 时,
时,![]() ,
,
解得:![]() ;
;
②当![]() 时,
时,![]() ,
,
解得:![]() .
.

练习册系列答案
相关题目
【题目】已知![]() 是
是![]() 的反比例函数,下表给出了
的反比例函数,下表给出了![]() 与
与![]() 的一些值.
的一些值.
| … | -4 | -2 | -1 | 1 | 3 | 4 | … | ||
| … | -2 | 6 | 3 | … |
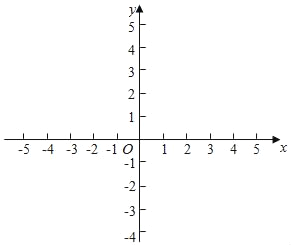
(1)求出这个反比例函数的表达式;
(2)根据函数表达式完成上表;
(3)根据上表,在下图的平面直角坐标系中作出这个反比例函数的图象.