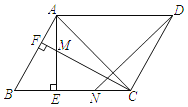
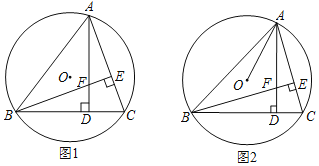
题目内容
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,动点
,动点![]() 从点
从点![]() 出发,在
出发,在![]() 边上以每秒2
边上以每秒2![]() 的速度向点
的速度向点![]() 匀速运动,同时动点
匀速运动,同时动点![]() 从点
从点![]() 出发,在
出发,在![]() 边上以每秒
边上以每秒![]()
![]() 的速度向点
的速度向点![]() 匀速运动,设运动时间为
匀速运动,设运动时间为![]() (
(![]() ),连接
),连接![]() .
.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)若![]() 与
与![]() 相似,求
相似,求![]() 的值;
的值;
(3)当![]() 为何值时,四边形
为何值时,四边形![]() 的面积最小?并求出最小值.
的面积最小?并求出最小值.

【答案】(1) ![]() ;(2)
;(2)![]() 或
或![]() ;(3) 当
;(3) 当![]() 时,
时,![]() 取最小值,
取最小值,![]() .
.
【解析】
(1)由已知条件得出AB=10,BC=5![]() ,由题意知BM=2t,CN=
,由题意知BM=2t,CN=![]() t,BN=5
t,BN=5![]()
![]() t,由BM=BN得出方程2t=5
t,由BM=BN得出方程2t=5![]()
![]() t,解方程即可;
t,解方程即可;
(2)分两种情况:①当△MBN∽△ABC时,由相似三角形的对应边成比例得出比例式,即可得出t的值;
②当△NBM∽△ABC时,由相似三角形的对应边成比例得出比例式,即可得出t的值;
(3)过M作MD⊥BC于点D,则MD∥AC,证出△BMD∽△BAC,得出比例式求出MD=t;四边形ACNM的面积y=△ABC的面积-△BMN的面积,得出y是t的二次函数,由二次函数的性质即可得出结果.
解:(1)在![]() 中,∵
中,∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() .
.
由题意知![]() ,
,![]() ,
,
∴![]() .
.
由![]() ,得
,得![]() .
.
解得![]() ;
;
(2)①当![]() ∽
∽![]() 时,
时,
得![]() ,即
,即![]()
解得![]() ;
;
②当![]() ∽
∽![]() 时,
时,
得![]() ,即
,即![]()
解得![]()
∴当![]() 或
或![]() 时,
时,![]() 与
与![]() 相似;
相似;
(3)如图,过点![]() 作
作![]() 于点
于点![]() ,则
,则![]() .
.
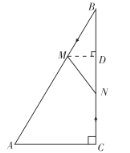
设四边形![]() 的面积为
的面积为![]() .
.
由题意,得![]()
![]()
![]()
![]()
∵![]()
∴当![]() 时,
时,![]() 取最小值,
取最小值,![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】一只不透明的袋子中装有![]() 个质地、大小均相同的小球,这些小球分别标有数字
个质地、大小均相同的小球,这些小球分别标有数字![]() ,甲、乙两人每次同时从袋中各随机摸出
,甲、乙两人每次同时从袋中各随机摸出![]() 个球,并计算摸出的这
个球,并计算摸出的这![]() 个小球上数字之和,记录后都将小球放回袋中搅匀,进行重复实验.实验数据如下表
个小球上数字之和,记录后都将小球放回袋中搅匀,进行重复实验.实验数据如下表
摸球总次数 |
|
|
|
|
|
|
|
|
|
|
“和为 |
|
|
|
|
|
|
|
|
|
|
“和为 |
|
|
|
|
|
|
|
|
|
|
解答下列问题:
![]() 如果实验继续进行下去,根据上表数据,出现“和为
如果实验继续进行下去,根据上表数据,出现“和为![]() ”的频率将稳定在它的概率附近.估计出现“和为
”的频率将稳定在它的概率附近.估计出现“和为![]() ”的概率是_______;
”的概率是_______;
![]() 如果摸出的这两个小球上数字之和为
如果摸出的这两个小球上数字之和为![]() 的概率是
的概率是![]() ,那么
,那么![]() 的值可以取
的值可以取![]() 吗?请用列表法或画树状图法说明理由;如果
吗?请用列表法或画树状图法说明理由;如果![]() 的值不可以取
的值不可以取![]() ,请写出一个符合要求的
,请写出一个符合要求的![]() 值.
值.