Question

【题目】如图，在矩形ABCD中，对角线AC，BD相交于点O，E是CD的中点，连接OE．过点C作CF∥BD交线段OE的延长线于点F，连接DF．

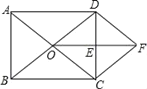
求证：（1）△ODE≌△FCE；

（2）四边形ODFC是菱形．

Answer 1

【答案】（1）证明见解析；（2）证明见解析．

【解析】

（1）根据两直线平行，内错角相等可得∠ODE=∠FCE，根据线段中点的定义可得CE=DE，然后利用“角边角”证明△ODE和△FCE全等；

（2）根据全等三角形对应边相等可得OD=FC，再根据一组对边平行且相等的四边形是平行四边形判断出四边形ODFC是平行四边形，根据矩形的对角线互相平分且相等可得OC=OD，然后根据邻边相等的平行四边形是菱形证明即可．

（1）∵CF∥BD，∴∠ODE=∠FCE．

∵E是CD中点，∴CE=DE．在△ODE和△FCE中，∵，∴△ODE≌△FCE（ASA）；

（2）∵△ODE≌△FCE，∴OD=FC．

∵CF∥BD，∴四边形ODFC是平行四边形，在矩形ABCD中，OC=OD，∴四边形ODFC是菱形．