Question

【题目】（探究函数的图象与性质）

（1）函数的自变量x的取值范围是________；

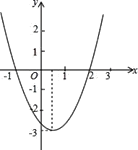
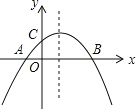
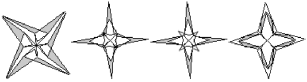
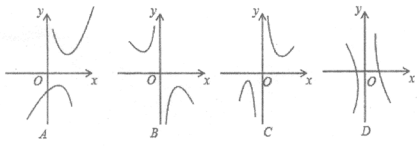
（2）下列四个函数图象中，函数的图象大致是_______；

（3）对于函数，求当x>0时，y的取值范围。请将下面求解此问题的过程补充完整：

解：因为x>0，所以_________。

因为，所以y________。

（拓展运用）

（4）若函数，则y的取值范围是_______________________。

Answer 1

【答案】（1）x≠0；（2）C；（3）6，y≥6；（4）y≤－11或y≥1.

【解析】

（1）由中x≠0，即可得出函数y=x+的自变量x的取值范围；
（2）由x≠0可排除A选项，再由y与x同号，可知函数y=x+的图象在第一、三象限，由此即可得出结论；
（3）根据用配方法求y值的范围的过程补充完整解题过程，即可得出结论；
（4）将变成y=x+-5，由（3）的结论可得出y=x+中y的取值范围为y≤-6或y≥6，在此基础上减去5即可得出结论．

解：（1）∵在y=x+中，x≠0，
∴x的取值范围是x≠0．
故答案为：x≠0；
（2）∵x≠0，
∴A中图象不符合题意；
∵当x＞0时，x+＞0，
当x＜0时，x+＜0，
∴函数y=x+的图象在第一、三象限，
∴B、D中图象不符合题意，
故选C．
（3）解：∵x＞0，
∴y=x+，
6，
∵，
∴y≥6．
故答案为：6；≥6．
（4）=x+-5．
由（3）可知：当x＞0时，x+≥6；
当x＜0时，x+≤-6．
∴y=x+-5≥6-5=1，y=x+-5≤-6-5=-11．
y的取值范围是y≤-11或y≥1．
故答案为：（1）x≠0；（2）C；（3）6，y≥6；（4）y≤-11或y≥1．