Question

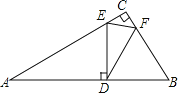
【题目】如图，在一块直角三角板ABC中，∠C=90°，∠A=30°，BC=1，将另一个含30°角的△EDF的30°角的顶点D放在AB边上，E、F分别在AC、BC上，当点D在AB边上移动时，DE始终与AB垂直，若△CEF与△DEF相似，则AD= ．

Answer 1

【答案】或

【解析】

试题由于∠EDF=30°，且DE总垂直于AB，因此∠FDB=60°，此时发现△FDB是等边三角形，那么BD=BF，2﹣AD=1﹣CF，即AD=CF+1．由于∠C是直角，当△CEF与△DEF相似时，△DEF必为直角三角形，那么可分两种情况讨论：①∠DEF=90°，此时，△CEF∽△DEF；②∠DFE=90°，此时△CEF∽△FED；可根据各相似三角形得到的比例线段求出CF的值，进而可求得AD的值．

解：∵∠EDF=30°，ED⊥AB于D，

∴∠FDB=∠B=60°，

∴△BDF是等边三角形；

∵BC=1，∴AB=2；

∵BD=BF，

∴2﹣AD=1﹣CF；

∴AD=CF+1．

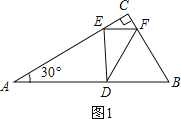
①如图1，∠FED=90°，△CEF∽△EDF，

∴=，即=，

解得，CF=；

∴AD=+1=；

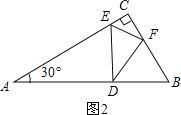
②如图2，∠EFD=90°，△CEF∽△FED，

∴=，即=；

解得，CF=；

∴AD=+1=．

故答案为或．