题目内容
15. 如图,等边△ABC的边长为4cm,点P从点A出发,以1cm/s的速度向点C移动,同时点Q从点A出发,以2cm/s的速度沿AB-BC的方向向点C移动,若△APQ的面积为S(cm2),则下列最能反映S(cm2)与移动时间t(s)之间函数关系的大致图象是( )
如图,等边△ABC的边长为4cm,点P从点A出发,以1cm/s的速度向点C移动,同时点Q从点A出发,以2cm/s的速度沿AB-BC的方向向点C移动,若△APQ的面积为S(cm2),则下列最能反映S(cm2)与移动时间t(s)之间函数关系的大致图象是( )| A. |  | B. |  | C. | 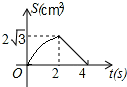 | D. |  |
分析 当点Q在AB上时,根据题意可知△APQ为直角三角形,然后根据三角形的面积公式列出函数关系式,当点Q在BC上时,△QAP为直角三角形,然后根据三角形的面积公式可求得S与t的函数关系式.
解答 解:当点Q在AB上时,如图1所示: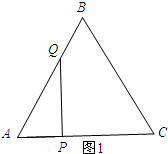
∵QA=2t,PA=t,
∴$\frac{AP}{QA}$=$\frac{1}{2}$.
∵∠A=60°,
∴cos∠A=$\frac{1}{2}$.
∴cos∠A=$\frac{AP}{AQ}$.
∴QP⊥AP.
∴△APQ为直角三角形.
∵AP=t,∠A=60°,
∴QP=$\sqrt{3}t$.
∴${S}_{△APQ}=\frac{1}{2}AP•QP$=$\frac{1}{2}×t×\sqrt{3}t$=$\frac{\sqrt{3}}{2}{t}^{2}$(0<t≤2).
当点Q在AB上时,如图2所示: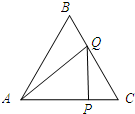
由题意可知:AP=t,PC=(4-t),
∵QC=8-2t,PC=4-t,
∴$\frac{PC}{QC}=\frac{1}{2}$.
∵∠C=60°,
∴cos∠C=$\frac{1}{2}$.
∴cos∠C=$\frac{QC}{PC}$.
∴QP⊥PC.
∴PQ=tan∠C•PC=$\sqrt{3}$(4-t).
∴${S}_{△AQP}=\frac{1}{2}AP•QP$=$\frac{1}{2}×t×\sqrt{3}(4-t)$=$-\frac{\sqrt{3}}{2}{t}^{2}+2\sqrt{3}t$.
故选:B.
点评 本题主要考查的是动点问题的函数图象,根据题意求得△APQ的面积与t的函数关系式是解题的关键.

练习册系列答案
相关题目
10.图中是正方体的平面展开图的是( )
| A. |  | B. |  | C. |  | D. |  |
 如图,方格纸中的每个小方格都是边长为1个单位的正方形,建立平面直角坐标系后,△ABC的顶点都在格点上,点C的坐标为(0,-1).
如图,方格纸中的每个小方格都是边长为1个单位的正方形,建立平面直角坐标系后,△ABC的顶点都在格点上,点C的坐标为(0,-1). 如图,直角梯形ABCD中,AB∥CD,AB⊥AD,BC=BA.
如图,直角梯形ABCD中,AB∥CD,AB⊥AD,BC=BA.