题目内容
20. 如图,直角梯形ABCD中,AB∥CD,AB⊥AD,BC=BA.
如图,直角梯形ABCD中,AB∥CD,AB⊥AD,BC=BA.(1)求证:以A为圆心,AD为半径的圆与BC相切;
(2)若AD=5,CD=2,求梯形ABCD的面积.
分析 (1)如图1,过A作AM⊥BC于M,求出∠DCA=∠ACB,根据角平分线性质求出AD=AM,根据切线的判定得出即可;
(2)如图2,过C作CN⊥AB于N,根据勾股定理得出方程,求出AB,根据梯形的面积公式求出即可.
解答 (1)证明:如图1,过A作AM⊥BC于M,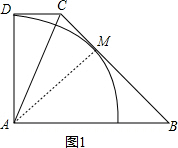
∵DC∥AB,
∴∠DCA=∠CAB,
∵BC=BA,
∴∠CAB=∠ACB,
∴∠DCA=∠ACB,
∵AB∥CD,AB⊥AD,
∴AD⊥DC,
∴AD=AM,
∵AM⊥BC,
∴以A为圆心,AD为半径的圆与BC相切;
(2)解:如图2,过C作CN⊥AB于N,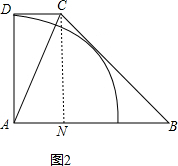
∵AD⊥AB,AD⊥DC,
∴∠CNB=90°,∠CDA=∠DAN=∠ANC=90°,
∴四边形ADCN是矩形,
∴AD=NC=5,CD=AN=2,
由勾股定理得:CN2+BN2=BC2,
52+(AB-2)2=AB2,
解得:AB=$\frac{29}{4}$.
∴梯形ABCD的面积是$\frac{1}{2}$×(CD+AB)×AD=$\frac{1}{2}$×(2+$\frac{29}{4}$)×5=$\frac{185}{8}$.
点评 本题考查了切线的判定,勾股定理,矩形的性质和判定,角平分线性质的应用,能正确作出辅助线是解此题的关键.

练习册系列答案
相关题目
5.“十•一”黄金周期间,威海华夏城在7天假期中每天接待游客的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数)
(1)若9月30日的游客人数为1.2千人,则10月2日的游客人数为2.6千人;
(2)七天内游客人数最多的一天是10月4日,人数达到2.8千人.
(3)若门票每人80元,请求出黄金周期间威海华夏城门票总收入是多少万元?
| 日期 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
| 人数变化(千人) | +0.6 | +0.8 | -0.4 | +0.6 | -0.8 | +0.2 | -1.4 |
(2)七天内游客人数最多的一天是10月4日,人数达到2.8千人.
(3)若门票每人80元,请求出黄金周期间威海华夏城门票总收入是多少万元?
12.我校九年级举行一次数学月考,其中7位同学的成绩如下:90,91,80,90,90,80,95.则这七个数据的众数、中位数是( )
| A. | 80、90 | B. | 85、90 | C. | 90、88 | D. | 90、90 |
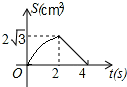
 如图,等边△ABC的边长为4cm,点P从点A出发,以1cm/s的速度向点C移动,同时点Q从点A出发,以2cm/s的速度沿AB-BC的方向向点C移动,若△APQ的面积为S(cm2),则下列最能反映S(cm2)与移动时间t(s)之间函数关系的大致图象是( )
如图,等边△ABC的边长为4cm,点P从点A出发,以1cm/s的速度向点C移动,同时点Q从点A出发,以2cm/s的速度沿AB-BC的方向向点C移动,若△APQ的面积为S(cm2),则下列最能反映S(cm2)与移动时间t(s)之间函数关系的大致图象是( )