题目内容
4. 用一张长为10m的梯子斜靠在墙上,梯子的顶端距墙角8m.
用一张长为10m的梯子斜靠在墙上,梯子的顶端距墙角8m.(1)梯子底端距墙角有6米;
(2)若梯子底端下滑1m,则梯子的底端水平滑动多少米?
分析 (1)直接利用勾股定理得出梯子底端距墙角的距离;
(2)设梯子的底端水平滑动x米,再利用勾股定理得出答案.
解答 解:(1)由题意可得:
梯子底端距墙角有:$\sqrt{1{0}^{2}-{8}^{2}}$=6(m).
故答案为:6;
(2)设梯子的底端水平滑动x米,根据题意可得:
(x+6)2+72=102,
解得:x1=-6+$\sqrt{51}$,x2=-6-$\sqrt{51}$(负数舍去).
答:梯子的底端水平滑动(-6+$\sqrt{51}$)米.
点评 此题主要考查了勾股定理的应用以及一元二次方程的解法,正确应用勾股定理得出第3边长是解题关键.

练习册系列答案
相关题目
19.下列各式是一元二次方程的是( )
| A. | 3-5x2=x | B. | $\frac{3}{x}$+x2-1=0 | C. | ax2+bx+c=0 | D. | 4x-1=0 |
16.下列对“0”说法不正确的是( )
| A. | 0既不是正数,也不是负数 | B. | 0是最小的整数 | ||
| C. | 0是整数,也是有理 | D. | 0是有理数,也叫中性数 |
13.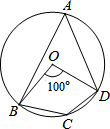 如图,四边形ABCD为⊙O的内接四边形,已知∠BOD=100°,则∠BCD的度数为( )
如图,四边形ABCD为⊙O的内接四边形,已知∠BOD=100°,则∠BCD的度数为( )
 如图,四边形ABCD为⊙O的内接四边形,已知∠BOD=100°,则∠BCD的度数为( )
如图,四边形ABCD为⊙O的内接四边形,已知∠BOD=100°,则∠BCD的度数为( )| A. | 130° | B. | 100° | C. | 80° | D. | 50° |
14.下列方程,是一元二次方程的是( )
①3x2+x=20,②2x2-3xy+4=0,③x2-x=4,④x2=0,⑤x2-x+3=0.
①3x2+x=20,②2x2-3xy+4=0,③x2-x=4,④x2=0,⑤x2-x+3=0.
| A. | ①② | B. | ①③④⑤ | C. | ①③④ | D. | ①④⑤ |