题目内容
5. 如图,在△ABC中,DE∥BC,AD=2BD,AE=5.求:
如图,在△ABC中,DE∥BC,AD=2BD,AE=5.求:(1)$\frac{AC}{AF}$;
(2)AC的值.
分析 (1)根据平行线分线段成比例定理,由DG∥BF得到$\frac{AG}{AF}$=$\frac{AD}{AB}$,然后利用AD=2BD可计算出$\frac{AG}{AF}$的值;
(2)根据平行线分线段成比例定理,由DE∥BC得到$\frac{AE}{AC}$=$\frac{AD}{AB}$=$\frac{2}{3}$,然后把AE=5代入可计算出AC的长.
解答 解:(1)∵DG∥BF,
∴$\frac{AG}{AF}$=$\frac{AD}{AB}$,
而AD=2BD,
∴$\frac{AG}{AF}$=$\frac{2BD}{2BD+BD}$=$\frac{2}{3}$;
(2)∵DE∥BC,
∴$\frac{AE}{AC}$=$\frac{AD}{AB}$=$\frac{2}{3}$,
∴AC=$\frac{3}{2}$×5=$\frac{15}{2}$.
点评 本题考查了平行线分线段成比例:三条平行线截两条直线,所得的对应线段成比例.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
15.在实数-2,0,$\frac{1}{2}$,-π中,最小的一个实数是( )
| A. | -2 | B. | 0 | C. | $\frac{1}{2}$ | D. | -π |
20.若|a|与|b|互为相反数,|c|=3,且数c代表的点C在数轴原点的右侧,则a-b+c的值为( )
| A. | 4 | B. | -3 | C. | 3 | D. | ±3 |
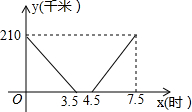 甲、乙两地相距210千米,一辆货车将货物由甲地运至乙地,卸载后返回甲地.若货车距乙地的距离y(千米)与时间t(时)的关系如图所示,根据所提供的信息,回答下列问题:
甲、乙两地相距210千米,一辆货车将货物由甲地运至乙地,卸载后返回甲地.若货车距乙地的距离y(千米)与时间t(时)的关系如图所示,根据所提供的信息,回答下列问题: 如图是一个计算程序,若输入a的值为-2,则输出的结果应为-2008.
如图是一个计算程序,若输入a的值为-2,则输出的结果应为-2008. 如图,在平面直角坐标系中,A(0,2),B(-2,4),C(-1,-2).试分别作出△ABC关于直线m:x=1和直线n;y=-1的对称图形,并写出对应顶点的坐标.
如图,在平面直角坐标系中,A(0,2),B(-2,4),C(-1,-2).试分别作出△ABC关于直线m:x=1和直线n;y=-1的对称图形,并写出对应顶点的坐标.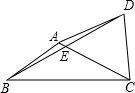 如图,在四边形ABCD中,对角线AC、BD交于点E,点E为BD的中点,∠BAC+∠BDC=180°,AB=CD=5,tan∠ACB=$\frac{1}{2}$,则AD=2$\sqrt{10}$.
如图,在四边形ABCD中,对角线AC、BD交于点E,点E为BD的中点,∠BAC+∠BDC=180°,AB=CD=5,tan∠ACB=$\frac{1}{2}$,则AD=2$\sqrt{10}$.