题目内容
14. 在平面直角坐标系中,抛物线y=x2-6mx+5与y轴的交点为A,与x轴的正半轴分别交于点B(b,0),C(c,0).
在平面直角坐标系中,抛物线y=x2-6mx+5与y轴的交点为A,与x轴的正半轴分别交于点B(b,0),C(c,0).(1)当b=1时,求抛物线相应的函数表达式;
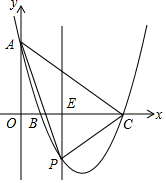
(2)当b=1时,如图,E(t,0)是线段BC上的一动点,过点E作平行于y轴的直线l与抛物线的交点为P.求△APC面积的最大值;
(3)当c=b+n时,且n为正整数,线段BC(包括端点)上有且只有五个点的横坐标是整数,求b的值.
分析 (1)当b=1时,将点B(1,0)代入抛物线y=x2-6mx+5中求出m,即可解决问题.
(2)如图1中,直线AC与PE交于点F.切线直线AC的解析式,构建二次函数,利用二次函数的性质即可解决问题.
(3)分两种情形①当b整数时,n为整数,可知n=4,c=b+4.则b,b+4是方程x2-mx+5=0的两个根,分别代入方程中求解即可,②当b小数时,n为整数,∴n=5,c=b+5为小数,则b,b+5是方程x2-6x+5=0的两个根,
解答 解:(1)当b=1时,将点B(1,0)代入抛物线y=x2-6mx+5中,得m=1,
∴y=x2-6x+5;
(2)如图1中,直线AC与PE交于点F.
当b=1时,求得A(0,5),B(1,0),C(5,0),可得AC所在的一次函数表达式为y=-x+5,
∵E(t,0),
∴P (t,t2-6t+5),直线l与AC的交点为F(t,-t+5),
∴PF=(-t+5)-(t2-6t+5)=-t2+5t,
∴S△APC=$\frac{1}{2}$×(-t2+5t)•5=-$\frac{5}{2}$(t-$\frac{5}{2}$)2+$\frac{125}{8}$,
∵-$\frac{5}{2}$<0,
∴当t=$\frac{5}{2}$时,面积S有最大值$\frac{125}{8}$;
(3)①当b整数时,n为整数,
∴n=4,c=b+4.则b,b+4是方程x2-mx+5=0的两个根,分别代入方程中,
得b2-mb+5=0 ①,(b+4)2-m(b+4)+5=0 ②,
由①②可得b2+4b-5=0,解得b=1或-5(舍);
或由一元二次方程根与系数的关系得 b(b+4)=5解得b=1或-5(舍).
②当b小数时,n为整数,∴n=5,c=b+5为小数,则b,b+5是方程x2-mx+5=0的两个根,同样可得b=$\frac{-5+3\sqrt{5}}{2}$或$\frac{-5-3\sqrt{5}}{2}$(舍弃);
∴b=1或$\frac{-5+3\sqrt{5}}{2}$.
点评 本题考查二次函数综合题、一次函数、最值问题、一元二次方程等知识,解题的关键是熟练应用思想知识解决问题,学会构建二次函数解决最值问题,学会用分类讨论的思想思考问题,属于不能漏解,属于中考压轴题.

 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
| A. | 平均数 | B. | 众数 | C. | 中位数 | D. | 方差 |