题目内容
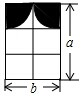 如图,窗户由六个小正方形组成,某饰物是两个四分之一圆.
如图,窗户由六个小正方形组成,某饰物是两个四分之一圆.(1)请用含a(或b)的式子表示能射进阳光的部分;
(2)当a=120cm,b=80cm时,求能射入阳光部分的面积.
考点:列代数式,代数式求值
专题:
分析:(1)由题意可知,装饰物正好是以
b为半径的一半圆,窗户中能射进阳光部分的面积正好是窗户的面积减去这个半圆的面积;
(2)将a=120cm,b=80cm代入(1)中所求代数式,计算即可求解.
| 1 |
| 2 |
(2)将a=120cm,b=80cm代入(1)中所求代数式,计算即可求解.
解答:解:(1)窗户中能射进阳光部分的面积=ab-
π(
b)2=ab-
b2;
(2)当a=120cm,b=80cm时,
窗户中能射进阳光部分的面积=120×80-
×802=9600-800π(cm2).
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 8 |
(2)当a=120cm,b=80cm时,
窗户中能射进阳光部分的面积=120×80-
| π |
| 8 |
点评:此题考查了列代数式与代数式求值,关键是要知道射进阳光部分的面积正好是窗户的面积减去这个半圆的面积.

练习册系列答案
相关题目
若a+b+c=0,那么一元二次方程ax2+bx+c=0必有一根是( )
| A、O | B、1 | C、-1 | D、2 |
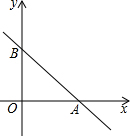 在平面直角坐标系中,一次函数的图象与坐标轴围成的三角形,叫做此一次函数的坐标三角形.例如,图中的一次函数的图象与x轴、y轴分别交于点A、B,则△OAB为此函数的坐标三角形.
在平面直角坐标系中,一次函数的图象与坐标轴围成的三角形,叫做此一次函数的坐标三角形.例如,图中的一次函数的图象与x轴、y轴分别交于点A、B,则△OAB为此函数的坐标三角形.