题目内容
如图，D为△ABC一点，AB=AC，BC=CD，∠ABD=15°，则∠A=________°．
40
分析：设∠A=x．根据三角形的外角的性质，得∠BDC=15+x，根据等腰三角形的性质，得∠CBD=∠CDB=15+x，则∠ABC=30+x，再根据等腰三角形的性质，得∠ACB=∠ABC=30+x，再根据三角形的内角和定理列方程求解．
解答：设∠A=x．
∵BC=CD，∠ABD=15°，
∴∠CBD=∠CDB=15+x．
∵AB=AC，
∴∠ACB=∠ABC=30+x．
∴x+2（30+x）=180°，
x=40°．
即∠A=40°．
点评：此题综合运用了等腰三角形的性质和三角形的内角和定理及其推论．
分析：设∠A=x．根据三角形的外角的性质，得∠BDC=15+x，根据等腰三角形的性质，得∠CBD=∠CDB=15+x，则∠ABC=30+x，再根据等腰三角形的性质，得∠ACB=∠ABC=30+x，再根据三角形的内角和定理列方程求解．
解答：设∠A=x．
∵BC=CD，∠ABD=15°，
∴∠CBD=∠CDB=15+x．
∵AB=AC，
∴∠ACB=∠ABC=30+x．
∴x+2（30+x）=180°，
x=40°．
即∠A=40°．
点评：此题综合运用了等腰三角形的性质和三角形的内角和定理及其推论．
练习册系列答案
优等生题库系列答案
53天天练系列答案
相关题目
认真阅读，并回答下面问题：
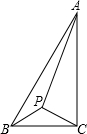（2013•松北区一模）如图，P为△ABC内一点，∠BAC=30°，∠ACB=90°，∠BPC=120°．若BP=
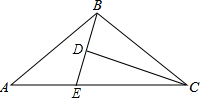（2013•邯郸一模）如图，D为△ABC内一点，CD平分∠ACB，BE⊥CD，垂足为D，交AC于点E，∠A=∠ABE．若AC=5，BC=3，则BD的长为（ ）
（2013•白云区一模）如图，D为△ABC的AB边上一点，E为AC延长线上的一点，且CE=BD．
如图，P为△ABC的边BC上的任意一点，设BC=a，BC边上的高AH为h．作△ABC的中位线B1C1，连接PB1、PC1；作△AB1C1的中位线B2C2，连接PB2、PC2；…；这样一直作下去，得到一组三角形：△PB1C1、△PB2C2、…、△PBnCn（n为正整数），则△PBnCn的面积为