题目内容
 光线a照射到平面镜CD上,然后在平面镜AB和CD之间来回反射,光线的反射角等于入射角.若已知∠1=52°,∠3=70°,则∠2是( )
光线a照射到平面镜CD上,然后在平面镜AB和CD之间来回反射,光线的反射角等于入射角.若已知∠1=52°,∠3=70°,则∠2是( )| A、52° | B、61° | C、65° | D、70° |
分析:根据题意得到∠1=∠6,∠3=∠5,∠2=∠4,则∠6=52°,∠5=70°,再根据三角形的内角和定理可求得∠7+∠8,从而得到∠8的度数,利用互余即可得到∠2.
解答:解:如图,
由光线的反射角等于入射角,利用等角的余角相等则∠1=∠6,∠3=∠5,∠2=∠4,
∵∠1=52°,∠3=70°,
∴∠6=52°,∠5=70°,
∴∠7+∠8=180°-∠6-∠5=180°-52°-70°=58°,
而∠7=∠8,
∴∠8=
×58°=29°,
∴∠2=90°-29°=61°.
故选B.

由光线的反射角等于入射角,利用等角的余角相等则∠1=∠6,∠3=∠5,∠2=∠4,
∵∠1=52°,∠3=70°,
∴∠6=52°,∠5=70°,
∴∠7+∠8=180°-∠6-∠5=180°-52°-70°=58°,
而∠7=∠8,
∴∠8=
| 1 |
| 2 |
∴∠2=90°-29°=61°.
故选B.
点评:本题考查了三角形的内角和定理:三角形的内角和为180°.也考查了等角的余角相等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
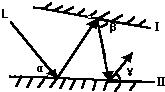 11、如图所示,光线L照射到平面镜I上,然后在平面镜Ⅰ、Ⅱ之间来回反射,已知∠α=55°,∠γ=75°,则∠β为( )
11、如图所示,光线L照射到平面镜I上,然后在平面镜Ⅰ、Ⅱ之间来回反射,已知∠α=55°,∠γ=75°,则∠β为( ) 19、如图,光线a照射到平面镜CD上,然后在平面镜AB和CD之间来回反射,这时光线的入射角等于反射角,即∠1=∠6,∠5=∠3,∠2=∠4.若已知∠1=55°,∠3=75°,那么∠2等于
19、如图,光线a照射到平面镜CD上,然后在平面镜AB和CD之间来回反射,这时光线的入射角等于反射角,即∠1=∠6,∠5=∠3,∠2=∠4.若已知∠1=55°,∠3=75°,那么∠2等于
 如图,光线a照射到平面镜CD上,然后在平面镜AB和CD之间来回反射,这时光线的入射角等于反射角.若已知∠1=55°,∠3=65°,则∠2=
如图,光线a照射到平面镜CD上,然后在平面镜AB和CD之间来回反射,这时光线的入射角等于反射角.若已知∠1=55°,∠3=65°,则∠2=