题目内容
10. 如图,已知抛物线y=x2-(m+3)x+9的顶点C在x轴正半轴上,一次函数y=x+3与抛物线交于A、B两点,与x、y轴分别交于D、E两点
如图,已知抛物线y=x2-(m+3)x+9的顶点C在x轴正半轴上,一次函数y=x+3与抛物线交于A、B两点,与x、y轴分别交于D、E两点(1)求m的值;
(2)求A、B两点的坐标.
分析 (1)根据抛物线y=x2-(m+3)x+9的顶点C在x轴正半轴上,可得抛物线与x轴只有一个交点,所以△=0,据此求出m的值是多少即可.
(2)联立抛物线与一次函数的解析式,求出A、B两点的坐标各是多少即可.
解答 解:(1)∵抛物线y=x2-(m+3)x+9的顶点C在x轴正半轴上,
∴抛物线与x轴只有一个交点,
∴(m+3)2-4×9=0,
解得m=3或m=-9,
又∵-$\frac{-(m+3)}{2}$>0,
∴m>-3,
∴m=3.
(2)由(1),可得m=3,
∴抛物线的解析式为:y=x2-6x+9,
联立$\left\{\begin{array}{l}{y{=x}^{2}-6x+9}\\{y=x+3}\end{array}\right.$
解得$\left\{\begin{array}{l}{x=1}\\{y=4}\end{array}\right.$或$\left\{\begin{array}{l}{x=6}\\{y=9}\end{array}\right.$,
根据图示,可得A点的横坐标小于B点的横坐标,
∴A点的坐标是(1,4),B两点的坐标是(6,9).
点评 此题主要考查了二次函数的性质,以及二次函数与一次函数的交点问题,要熟练掌握.

练习册系列答案
相关题目
15.某学校计划租用6辆客车送240名师生参加一年一度的武汉杂技节,感受杂技艺术的魅力.现有甲、乙两种客车,它们的载客量和租金如表.
若领队老师从学校预支租车费用1650元,试问预支的租车费用能否有结余?若有结余,最多可结余多少元?
| 甲种客车 | 乙种客车 | |
| 载客量(人/辆) | 45 | 30 |
| 租金(元/辆) | 280 | 200 |
 已知在长方形ABCD中,AB=4,BC=12,O为BC上一点,BO=3.如图所示,O为坐标原点建立平面直角坐标系.若点M坐标为(5,0),点N在长方形边上,且△OMN为等腰三角形,求出所有符合要求的点N的坐标.
已知在长方形ABCD中,AB=4,BC=12,O为BC上一点,BO=3.如图所示,O为坐标原点建立平面直角坐标系.若点M坐标为(5,0),点N在长方形边上,且△OMN为等腰三角形,求出所有符合要求的点N的坐标.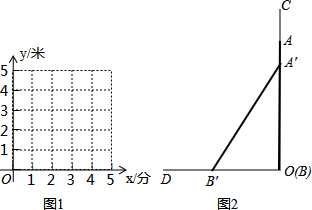
 匀速地向如图所示的容器中注水,直到把容器注满,下列图线能大致反映水面高度h随注水时间t变化的是( )
匀速地向如图所示的容器中注水,直到把容器注满,下列图线能大致反映水面高度h随注水时间t变化的是( )



 皮影戏是中国民间古老的传统艺术,如图就是皮影戏中孙悟空的一个形象,在下面的四个图形中,能由图经过平移得到的图形是( )
皮影戏是中国民间古老的传统艺术,如图就是皮影戏中孙悟空的一个形象,在下面的四个图形中,能由图经过平移得到的图形是( )


