题目内容
18.关于x的一元二次方程(k-1)x2-2x+1=0总有实数根,则k应满足的条件是( )| A. | k≤2 | B. | k≤2且k≠1 | C. | k<2且k≠1 | D. | k≥2 |
分析 利用一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:①当△>0时,方程有两个不相等的两个实数根;②当△=0时,方程有两个相等的两个实数根;③当△<0时,方程无实数根;进而得出△=b2-4ac=4-4(k-1)≥0,再求出答案.
解答 解:∵关于x的一元二次方程(k-1)x2-2x+1=0总有实数根,
∴△=b2-4ac=4-4(k-1)≥0,
解得:k≤2,
且k-1≠0,
则k应满足的条件是:k≤2且k≠1.
故选:B.
点评 此题主要考查了根的判别式,正确得出关于k的不等关系是解题关键.

练习册系列答案
相关题目
3.下列运算正确的是( )
| A. | $\sqrt{(-5)^{2}}=-5$ | B. | 4$\sqrt{3}$-$\sqrt{27}$=1 | C. | $\sqrt{18}÷\sqrt{2}$=9 | D. | $\sqrt{24}•\sqrt{\frac{3}{2}}=6$ |
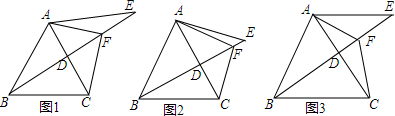
 如图,△ABC和△BDE都是等边三角形,如果∠ABE=40°.那么∠CBD的大小为40°.
如图,△ABC和△BDE都是等边三角形,如果∠ABE=40°.那么∠CBD的大小为40°.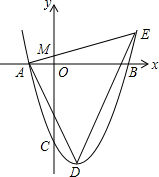 如图.抛物线y=x2一2x-8与x轴交于A、B两点,与y轴交于点C,D为抛物线的顶点,E为第一象限的抛物线上一点.且DE为△ADE的外接圆的直径,AD交y轴于F.
如图.抛物线y=x2一2x-8与x轴交于A、B两点,与y轴交于点C,D为抛物线的顶点,E为第一象限的抛物线上一点.且DE为△ADE的外接圆的直径,AD交y轴于F. ”表示每抛2次就有一次正面朝上
”表示每抛2次就有一次正面朝上 ”表示随着抛掷次数的增加,“抛出朝上的点数为2”这一事件发生的频率稳定在
”表示随着抛掷次数的增加,“抛出朝上的点数为2”这一事件发生的频率稳定在 附近
附近