题目内容
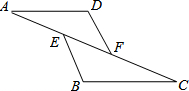如图，已知E、F是AC上的两点，AE=CF，DF=BE，∠AFD=∠CEB，则下列结论不成立的是（ ）| A、∠A=∠CEB |
| B、AD=CB |
| C、BE=DF |
| D、DF∥BE |
考点：全等三角形的判定与性质
专题：
分析：根据等式的性质，可得AF与CE的关系，根据全等三角形的判定与性质，可得答案．
解答：解：A、∠A=∠C，故A错误；
B、AE=CF，
∴AE+EF=CF+EF，即AF=CE，
在△AFD与△CEB中，
，
△AFD≌△CEB（SAS），
∴AD=CB，故B正确；
C、BE=DF，故C正确；
D、∵∠AFD=∠CEB，∴DF∥BE，故D正确；
故选：A．
B、AE=CF，
∴AE+EF=CF+EF，即AF=CE，
在△AFD与△CEB中，
|
△AFD≌△CEB（SAS），
∴AD=CB，故B正确；
C、BE=DF，故C正确；
D、∵∠AFD=∠CEB，∴DF∥BE，故D正确；
故选：A．
点评：本题考查了全等三角形的判定与性质，利用了全等三角形的判定与性质．
练习册系列答案
相关题目
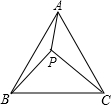如图，已知点P是等边△ABC内一点，PA=3，PB=4，PC=5，求∠APB的度数．
实数a，b在数轴上的位置如图所示，则
如图：在直角坐标系中有Rt△ABC，且A（3，0），B（5，0），C（3，3）；P为y轴上一点，当以P，O，B为顶点的三角形与以A，B，C为顶点的三角形相似时，求P点的坐标．