题目内容
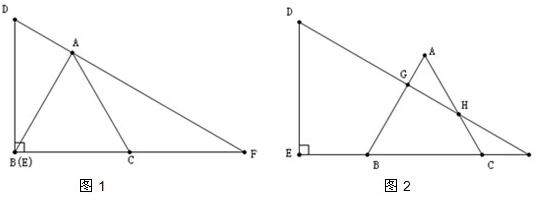
已知:△ABC是等边三角形,分别过点A,B作AF∥BC,BE∥AC,AF,BE分别与过点C的直线交于点F,E,连接线段BF,AE,BF交AE于点D
(1)求证:△AFC∽△BCE;
(2)△ABC的边长是3,AF=2,求BE的长;
(3)请你找出与△ABF相似的三角形,并证明.
 (1)证明:∵AF∥BC,
(1)证明:∵AF∥BC,∴∠AFC=∠BCE,∠CAF=∠ACB,
∵BE∥AC,
∴∠EBC=∠ACB,
∴∠CAF=∠EBC.
在△AFC与△BCE中,∵∠AFC=∠BCE,∠CAF=∠EBC,
∴△AFC∽△BCE;
(2)解:∵△AFC∽△BCE,
∴AF:BC=AC:BE,
∵等边△ABC的边长是3,
∴BC=AC=3,
又AF=2,
∴2:3=3:BE,
∴BE=
 ;
;(3)解:△BEA∽△ABF,理由如下:
∵△ABC是等边三角形,
∴∠BAC=∠ABC=∠ACB=60°.
∵∠ABE=∠ABC+∠EBC=∠ABC+∠ACB=120°,
∠FAB=∠CAF+∠BAC=∠ACB+∠BAC=120°,
∴∠ABE=∠FAB.
∵△BCE∽△AFC,
∴
 =
= ,
,∵AC=AB=BC,
∴
 =
= .
.在△BEA与△ABF中,∵
 =
= ,∠ABE=∠FAB,
,∠ABE=∠FAB,∴△BEA∽△ABF.
分析:(1)先由平行线的性质得出∠AFC=∠BCE,∠CAF=∠EBC,再根据两角对应相等,两三角形相似即可证明△AFC∽△BCE;
(2)由△AFC∽△BCE,根据相似三角形对应边成比例及等边三角形的性质即可求出BE的长;
(3)先根据等边三角形及平行线的性质得出∠ABE=∠FAB,再根据△BCE∽△AFC,得出
 =
= ,则由两边对应成比例且夹角相等,两三角形相似即可证明△BEA∽△ABF.
,则由两边对应成比例且夹角相等,两三角形相似即可证明△BEA∽△ABF.点评:本题主要考查了平行线的性质,等边三角形的性质,相似三角形的判定与性质,难度中等.其中(3)通过观察△ABF的形状,得出∠ABE=∠FAB=120°,再由△BCE∽△AFC,进而得出
 =
= 是解题的关键.
是解题的关键. 
练习册系列答案
相关题目
某“研究性学习小组”遇到了以下问题,请参与:
已知,△ABC是等边三角形且内接于⊙O,取
上异于A、B的点M.设直线CA与BM相交于点K,直线CB与AM相交于点N.
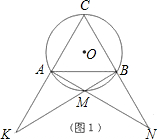

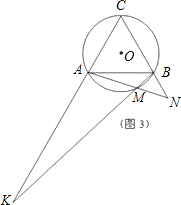
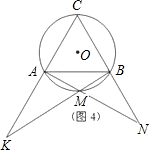
(1)如图1,图2,图3,M分别为
的中点、三分之一点、四分之一点,△ABC的边长均为2,分别测量出AK、BN的长,计算AK•BN的值(精确到0.01)并将结果填入下表中:
(2)如图4,当M为
上任意一点时,根据(1)的结果,猜想AK•BN与AB的数量关系式为 ;
(3)对(2)中提出的猜想,依图4给出证明.
已知,△ABC是等边三角形且内接于⊙O,取
 |
| AB |




(1)如图1,图2,图3,M分别为
 |
| AB |
| △ABC的边长 | AK•BN的值 | |
| 图1 | 2 | |
| 图2 | 2 | |
| 图3 | 2 |
 |
| AB |
(3)对(2)中提出的猜想,依图4给出证明.
 三个为条件,余下的一个为结论,组成一个正确的命题(只需写出一种),并给予证明.
三个为条件,余下的一个为结论,组成一个正确的命题(只需写出一种),并给予证明.
