题目内容
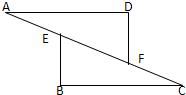
如图,现给出四个论断:①DB=DE;②CE=CD;③BD是△ABC的中线;④△ABC是等边三角形.请以其中的 三个为条件,余下的一个为结论,组成一个正确的命题(只需写出一种),并给予证明.
三个为条件,余下的一个为结论,组成一个正确的命题(只需写出一种),并给予证明.
已知:
求证:
证明:
 三个为条件,余下的一个为结论,组成一个正确的命题(只需写出一种),并给予证明.
三个为条件,余下的一个为结论,组成一个正确的命题(只需写出一种),并给予证明.已知:
△ABC是等边三角形
△ABC是等边三角形
,BD是△ABC中线
BD是△ABC中线
;CD=CE
CD=CE
.求证:
DB=DE
DB=DE
证明:
分析:根据等边三角形性质推出AB=BC,∠ABC=∠ACB=60°,根据等腰三角形性质求出∠DBC=30°,∠E=∠CDE,根据三角形外角性质求出∠E=30°,推出∠E=∠DBE即可.
解答:证明:∵三角形ABC是等边三角形,
∴AB=BC,∠ABC=∠ACB=60°,
∵BD是△ABC的中线,
∴∠DBC=
∠ABC=30°,
∵CD=CE,
∴∠E=∠CDE,
∵∠E+∠CDE=∠ACB=60°,
∴∠E=30°,
∴∠E=∠DBE,
∴DB=DE.
故答案为:△ABC是等边三角形,BD是△ABC的中线,CD=CE,DB=DE.
∴AB=BC,∠ABC=∠ACB=60°,
∵BD是△ABC的中线,
∴∠DBC=
| 1 |
| 2 |
∵CD=CE,
∴∠E=∠CDE,
∵∠E+∠CDE=∠ACB=60°,
∴∠E=30°,
∴∠E=∠DBE,
∴DB=DE.
故答案为:△ABC是等边三角形,BD是△ABC的中线,CD=CE,DB=DE.
点评:本题考查了等边三角形的性质,等腰三角形的性质,三角形的外角性质等知识点的应用,关键是求出∠E=∠DBC=30°,题目比较好,是一道开放性的题目,培养了学生的发散思维的能力.

练习册系列答案
相关题目
 23、如图,在△ADF与△CBE中,点A,E,F,C在同一直线上,现给出下列四个论断:①AE=CF;②AD=CB;③∠B=∠D;④AD∥BC.请你选择其中三个作为条件,余下的一个作为结论,构成一个命题.请问:
23、如图,在△ADF与△CBE中,点A,E,F,C在同一直线上,现给出下列四个论断:①AE=CF;②AD=CB;③∠B=∠D;④AD∥BC.请你选择其中三个作为条件,余下的一个作为结论,构成一个命题.请问: 三个为条件,余下的一个为结论,组成一个正确的命题(只需写出一种),并给予证明.
三个为条件,余下的一个为结论,组成一个正确的命题(只需写出一种),并给予证明.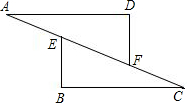 B;③∠B=∠D;④AD∥BC.请你选择其中三个作为条件,余下的一个作为结论,构成一个命题.请问:
B;③∠B=∠D;④AD∥BC.请你选择其中三个作为条件,余下的一个作为结论,构成一个命题.请问: