Question

【题目】平行四边形的对角线相交于点，的外接圆交于点且圆心恰好落在边上，连接，若.

（1）求证：为切线.

（2）求的度数.

（3）若的半径为1，求的长.

Answer 1

【答案】（1）详见解析;（2）;（3）

【解析】

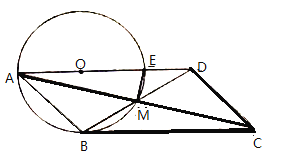
（1）连接OB，根据平行四边形的性质得到∠BAD＝∠BCD＝45°，根据圆周角定理得到∠BOD＝2∠BAD＝90°，根据平行线的性质得到OB⊥BC，即可得到结论；

（2）连接OM，根据平行四边形的性质得到BM＝DM，根据直角三角形的性质得到OM＝BM，求得∠OBM＝60°，于是得到∠ADB＝30°；

（3）连接EM，过M作MF⊥AE于F，根据等腰三角形的性质得到∠MOF＝∠MDF＝30°，根据OM＝OE＝1，解直角三角形即可得到结论．

（1）证明：连接OB，

∵四边形ABCD是平行四边形，

∴∠BAD＝∠BCD＝45°，

∴∠BOD＝2∠BAD＝90°，

∵AD∥BC，

∴∠DOB＋∠OBC＝180°，

∴∠OBC＝90°，

∴OB⊥BC，

∴BC为⊙O切线；

（2）解：连接OM，

∵四边形ABCD是平行四边形，

∴BM＝DM，

∵∠BOD＝90°，

∴OM＝BM，

∵OB＝OM，

∴OB＝OM＝BM，

∴∠OBM＝60°，

∴∠ADB＝30°；

（3）解：连接EM，过M作MF⊥AE于F，

∵OM＝DM，

∴∠MOF＝∠MDF＝30°，

∵的半径为1

∴OM＝OE＝1，

∴FM＝,OF＝，

∴EF＝1

故EM==．