ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ–ΓΟς¥ζ±μ―ß–Θ≤ΈΦ”ΓΑΈ“ΚΆΈ“ΒΡΉφΙζΓ±÷ςΧβ–ϊ¥ΪΫΧ”ΐΜνΕ·Θ§ΗΟΜνΕ·Ζ÷ΈΣΝΫΗωΫΉΕΈΘ§ΒΎ“ΜΫΉΕΈ”–ΓΑΗη«ζ―ί≥ΣΓ±ΓΔΓΑ ιΖ®’Ι ΨΓ±ΓΔΓΑΤςά÷ΕάΉύΓ±3ΗωœνΡΩΘ®“ά¥Έ”Ο![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() ±μ ΨΘ©Θ§ΒΎΕΰΫΉΕΈ”–ΓΑΙ ¬―ίΫ≤Γ±ΓΔΓΑ ΪΗηά Υ–Γ±2ΗωœνΡΩΘ®“ά¥Έ”Ο
±μ ΨΘ©Θ§ΒΎΕΰΫΉΕΈ”–ΓΑΙ ¬―ίΫ≤Γ±ΓΔΓΑ ΪΗηά Υ–Γ±2ΗωœνΡΩΘ®“ά¥Έ”Ο![]() ΓΔ
ΓΔ![]() ±μ ΨΘ©Θ§≤ΈΦ”»Υ‘±‘ΎΟΩΗωΫΉΕΈΗςΥφΜζ≥ι»Γ“ΜΗωœνΡΩΆξ≥….
±μ ΨΘ©Θ§≤ΈΦ”»Υ‘±‘ΎΟΩΗωΫΉΕΈΗςΥφΜζ≥ι»Γ“ΜΗωœνΡΩΆξ≥….
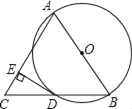
Θ®1Θ©”ΟΜ≠ ςΉ¥ΆΦΜρΝ–±μΒΡΖΫΖ®Θ§Ν–≥ω–ΓΟς≤ΈΦ”œνΡΩΒΡΥυ”–Β»Ω…ΡήΒΡΫαΙϊΘΜ
Θ®2Θ©«σ–ΓΟς«ΓΚΟ≥ι÷–![]() ΓΔ
ΓΔ![]() ΝΫΗωœνΡΩΒΡΗ≈¬ .
ΝΫΗωœνΡΩΒΡΗ≈¬ .
ΓΨ¥πΑΗΓΩΘ®1Θ©ΦϊΫβΈωΘΜΘ®2Θ©![]() .
.
ΓΨΫβΈωΓΩ
Θ®1Θ©Μ≠ ςΉ¥ΆΦΒΟ≥ωΥυ”–Β»Ω…ΡήΫαΙϊΘΜ
Θ®2Θ©¥”÷–’“ΒΫΖϊΚœΧθΦΰΒΡΫαΙϊ ΐΘ§‘ΌΗυΨίΗ≈¬ ΙΪ ΫΦΤΥψΩ…ΒΟΘ°
Θ®1Θ©Μ≠ ςΉ¥ΆΦ»γœ¬ΘΚ

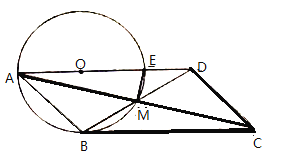
Θ®2Θ©”… ςΉ¥ΆΦ÷ΣΙ≤”–6÷÷Β»Ω…ΡήΫαΙϊΘ§Τδ÷––ΓΟς«ΓΚΟ≥ι÷–BΓΔDΝΫΗωœνΡΩΒΡ÷Μ”–1÷÷«ιΩωΘ§
Υυ“‘–ΓΟς«ΓΚΟ≥ι÷–BΓΔDΝΫΗωœνΡΩΒΡΗ≈¬ ΈΣΘΚ![]() Θ°
Θ°

 Οϊ≈Τ―ß–ΘΖ÷≤ψ÷ή÷ή≤βœΒΝ–¥πΑΗ
Οϊ≈Τ―ß–ΘΖ÷≤ψ÷ή÷ή≤βœΒΝ–¥πΑΗ ΜΤΗ‘ΚΘΒμ»Ϊ≥Χ≈ύ”≈≤β ‘ΨμœΒΝ–¥πΑΗ
ΜΤΗ‘ΚΘΒμ»Ϊ≥Χ≈ύ”≈≤β ‘ΨμœΒΝ–¥πΑΗΓΨΧβΡΩΓΩΩ’Φδ»Έ“β―ΓΕ®“ΜΒψ![]() Θ§“‘Βψ
Θ§“‘Βψ![]() ΈΣΕΥΒψΘ§Ής»ΐΧθΜΞœύ¥Ι÷±ΒΡ…δœΏ
ΈΣΕΥΒψΘ§Ής»ΐΧθΜΞœύ¥Ι÷±ΒΡ…δœΏ![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ°’β»ΐΧθΜΞœύ¥Ι÷±ΒΡ…δœΏΖ÷±π≥ΤΉς
Θ°’β»ΐΧθΜΞœύ¥Ι÷±ΒΡ…δœΏΖ÷±π≥ΤΉς![]() ÷αΓΔ
÷αΓΔ![]() ÷αΓΔ
÷αΓΔ![]() ÷αΘ§Ά≥≥ΤΈΣΉχ±ξ÷αΘ§ΥϋΟ«ΒΡΖΫœρΖ÷±πΈΣ
÷αΘ§Ά≥≥ΤΈΣΉχ±ξ÷αΘ§ΥϋΟ«ΒΡΖΫœρΖ÷±πΈΣ![]() Θ®Υ°ΤΫœρ«ΑΘ©Θ§
Θ®Υ°ΤΫœρ«ΑΘ©Θ§![]() Θ®Υ°ΤΫœρ”“Θ©Θ§
Θ®Υ°ΤΫœρ”“Θ©Θ§![]() Θ® ζ÷±œρ…œΘ©ΖΫœρΘ§’β―υΒΡΉχ±ξœΒ≥ΤΈΣΩ’Φδ÷±Ϋ«Ήχ±ξœΒΘ°ΫΪœύΝΎ»ΐΗωΟφΒΡΟφΜΐΦ«ΈΣ
Θ® ζ÷±œρ…œΘ©ΖΫœρΘ§’β―υΒΡΉχ±ξœΒ≥ΤΈΣΩ’Φδ÷±Ϋ«Ήχ±ξœΒΘ°ΫΪœύΝΎ»ΐΗωΟφΒΡΟφΜΐΦ«ΈΣ![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§«“
Θ§«“![]() ΒΡ–Γ≥ΛΖΫΧε≥ΤΈΣΒΞΈΜ≥ΛΖΫΧεΘ§œ÷ΫΪ»τΗ…ΗωΒΞΈΜ≥ΛΖΫΧε‘ΎΩ’Φδ÷±Ϋ«Ήχ±ξœΒΡΎΫχ––¬κΖ≈Θ§“Σ«σ¬κΖ≈ ±ΫΪΒΞΈΜ≥ΛΖΫΧε
ΒΡ–Γ≥ΛΖΫΧε≥ΤΈΣΒΞΈΜ≥ΛΖΫΧεΘ§œ÷ΫΪ»τΗ…ΗωΒΞΈΜ≥ΛΖΫΧε‘ΎΩ’Φδ÷±Ϋ«Ήχ±ξœΒΡΎΫχ––¬κΖ≈Θ§“Σ«σ¬κΖ≈ ±ΫΪΒΞΈΜ≥ΛΖΫΧε![]() Υυ‘ΎΒΡΟφ”κ
Υυ‘ΎΒΡΟφ”κ![]() ÷α¥Ι÷±Θ§
÷α¥Ι÷±Θ§![]() Υυ‘ΎΒΡΟφ”κ
Υυ‘ΎΒΡΟφ”κ![]() ÷α¥Ι÷±Θ§
÷α¥Ι÷±Θ§![]() Υυ‘ΎΒΡΟφ”κ
Υυ‘ΎΒΡΟφ”κ![]() ÷α¥Ι÷±Θ§»γΆΦ1Υυ ΨΘ°»τΫΪ
÷α¥Ι÷±Θ§»γΆΦ1Υυ ΨΘ°»τΫΪ![]() ÷αΖΫœρ±μ ΨΒΡΝΩ≥ΤΈΣΦΗΚΈΧε¬κΖ≈ΒΡ≈≈ ΐΘ§
÷αΖΫœρ±μ ΨΒΡΝΩ≥ΤΈΣΦΗΚΈΧε¬κΖ≈ΒΡ≈≈ ΐΘ§![]() ÷αΖΫœρ±μ ΨΒΡΝΩ≥ΤΈΣΦΗΚΈΧε¬κΖ≈ΒΡΝ– ΐΘ§Εΰ÷αΖΫœρ±μ ΨΒΡΝΩ≥ΤΈΣΦΗΚΈΧε¬κΖ≈ΒΡ≤ψ ΐΘΜ»γΆΦ2 «”…»τΗ…ΗωΒΞΈΜ≥ΛΖΫΧε‘ΎΩ’Φδ÷±Ϋ«Ήχ±ξΡΎ¬κΖ≈ΒΡ“ΜΗωΦΗΚΈΧεΘ§Τδ÷–’βΗωΦΗΚΈΧεΙ≤¬κΖ≈ΝΥ
÷αΖΫœρ±μ ΨΒΡΝΩ≥ΤΈΣΦΗΚΈΧε¬κΖ≈ΒΡΝ– ΐΘ§Εΰ÷αΖΫœρ±μ ΨΒΡΝΩ≥ΤΈΣΦΗΚΈΧε¬κΖ≈ΒΡ≤ψ ΐΘΜ»γΆΦ2 «”…»τΗ…ΗωΒΞΈΜ≥ΛΖΫΧε‘ΎΩ’Φδ÷±Ϋ«Ήχ±ξΡΎ¬κΖ≈ΒΡ“ΜΗωΦΗΚΈΧεΘ§Τδ÷–’βΗωΦΗΚΈΧεΙ≤¬κΖ≈ΝΥ![]() ≈≈
≈≈![]() Ν–
Ν–![]() ≤ψΘ§”Ο”––ρ ΐΉιΦ«Ής
≤ψΘ§”Ο”––ρ ΐΉιΦ«Ής![]() Θ§»γΆΦ3ΒΡΦΗΚΈΧε¬κΖ≈ΝΥ
Θ§»γΆΦ3ΒΡΦΗΚΈΧε¬κΖ≈ΝΥ![]() ≈≈
≈≈![]() Ν–
Ν–![]() ≤ψΘ§”Ο”––ρ ΐΉιΦ«Ής
≤ψΘ§”Ο”––ρ ΐΉιΦ«Ής![]() Θ°’β―υΈ“Ο«ΨΆΩ…”ΟΟΩ“ΜΗω”––ρ ΐΉι
Θ°’β―υΈ“Ο«ΨΆΩ…”ΟΟΩ“ΜΗω”––ρ ΐΉι![]() ±μ Ψ“Μ÷÷ΦΗΚΈΧεΒΡ¬κΖ≈ΖΫ ΫΘ°
±μ Ψ“Μ÷÷ΦΗΚΈΧεΒΡ¬κΖ≈ΖΫ ΫΘ°
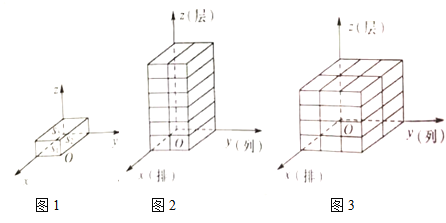
Θ®1Θ©”––ρ ΐΉι![]() ΥυΕ‘”ΠΒΡ¬κΖ≈ΒΡΦΗΚΈΧε «______________ΘΜ
ΥυΕ‘”ΠΒΡ¬κΖ≈ΒΡΦΗΚΈΧε «______________ΘΜ
A.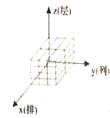 B.
B.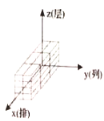 C.
C.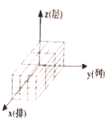 D.
D.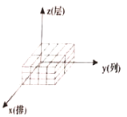
Θ®2Θ©ΆΦ4 «”…»τΗ…ΗωΒΞΈΜ≥ΛΖΫΧε¬κΖ≈ΒΡ“ΜΗωΦΗΚΈΧεΒΡ»ΐ ”ΆΦΘ§‘ρ’β÷÷¬κΖ≈ΖΫ ΫΒΡ”––ρ ΐΉιΈΣΘ®______Θ§_______Θ§_______Θ©Θ§Ήι≥…’βΗωΦΗΚΈΧεΒΡΒΞΈΜ≥ΛΖΫΧεΒΡΗω ΐΈΣ____________ΗωΘ°
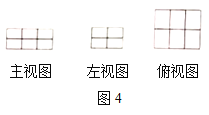
Θ®3Θ©ΈΣΝΥΫχ“Μ≤ΫΧΫΨΩ”––ρ ΐΉι![]() ΒΡΦΗΚΈΧεΒΡ±μΟφΜΐΙΪ Ϋ
ΒΡΦΗΚΈΧεΒΡ±μΟφΜΐΙΪ Ϋ![]() Θ§Ρ≥Ά§―ß’κΕ‘»τΗ…ΗωΒΞΈΜ≥ΛΖΫΧεΫχ––¬κΖ≈Θ§÷ΤΉςΝΥœ¬Ν–±μΗώΘΚ
Θ§Ρ≥Ά§―ß’κΕ‘»τΗ…ΗωΒΞΈΜ≥ΛΖΫΧεΫχ––¬κΖ≈Θ§÷ΤΉςΝΥœ¬Ν–±μΗώΘΚ
ΦΗΚΈΧε”––ρ ΐΉι | ΒΞΈΜ≥ΛΖΫΧεΒΡΗω ΐ | ±μΟφ…œΟφΜΐΈΣS1ΒΡΗω ΐ | ±μΟφ…œΟφΜΐΈΣS2ΒΡΗω ΐ | ±μΟφ…œΟφΜΐΈΣS3ΒΡΗω ΐ | ±μΟφΜΐ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ΗυΨί“‘…œΙφ¬…Θ§«κ÷±Ϋ”–¥≥ω”––ρ ΐΉι![]() ΒΡΦΗΚΈΧε±μΟφΜΐ
ΒΡΦΗΚΈΧε±μΟφΜΐ![]() ΒΡΦΤΥψΙΪ ΫΘΜΘ®”Ο
ΒΡΦΤΥψΙΪ ΫΘΜΘ®”Ο![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() ±μ ΨΘ©
±μ ΨΘ©
Θ®4Θ©Β±![]() Θ§
Θ§![]() Θ§
Θ§![]() ±Θ§Ε‘”…
±Θ§Ε‘”…![]() ΗωΒΞΈΜ≥ΛΖΫΧε¬κΖ≈ΒΡΦΗΚΈΧεΫχ––¥ρΑϋΘ§ΈΣΝΥΫΎ‘ΦΆβΑϋΉΑ≤ΡΝœΘ§Έ“Ο«Ω…“‘Ε‘
ΗωΒΞΈΜ≥ΛΖΫΧε¬κΖ≈ΒΡΦΗΚΈΧεΫχ––¥ρΑϋΘ§ΈΣΝΥΫΎ‘ΦΆβΑϋΉΑ≤ΡΝœΘ§Έ“Ο«Ω…“‘Ε‘![]() ΗωΒΞΈΜ≥ΛΖΫΧε¬κΖ≈ΒΡΦΗΚΈΧε±μΟφΜΐΉν–ΓΒΡΙφ¬…Ϋχ––ΧΫΨΩΘ§«κΡψΗυΨίΉ‘ΦΚΧΫΨΩΒΡΫαΙϊ÷±Ϋ”–¥≥ω ΙΦΗΚΈΧε±μΟφΜΐΉν–ΓΒΡ”––ρ ΐΉιΘ§’βΗω”––ρ ΐΉιΈΣΘ®______Θ§_______Θ§ ______Θ©Θ§¥Υ ±«σ≥ωΒΡ’βΗωΦΗΚΈΧε±μΟφΜΐΒΡ¥σ–ΓΈΣ____________Θ®ΖλœΕ≤ΜΦΤΘ©
ΗωΒΞΈΜ≥ΛΖΫΧε¬κΖ≈ΒΡΦΗΚΈΧε±μΟφΜΐΉν–ΓΒΡΙφ¬…Ϋχ––ΧΫΨΩΘ§«κΡψΗυΨίΉ‘ΦΚΧΫΨΩΒΡΫαΙϊ÷±Ϋ”–¥≥ω ΙΦΗΚΈΧε±μΟφΜΐΉν–ΓΒΡ”––ρ ΐΉιΘ§’βΗω”––ρ ΐΉιΈΣΘ®______Θ§_______Θ§ ______Θ©Θ§¥Υ ±«σ≥ωΒΡ’βΗωΦΗΚΈΧε±μΟφΜΐΒΡ¥σ–ΓΈΣ____________Θ®ΖλœΕ≤ΜΦΤΘ©
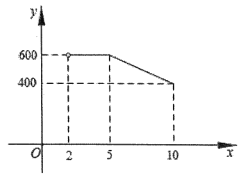
ΓΨΧβΡΩΓΩΈΣ”≠Ϋ”ΓΑ άΫγΜΣ»Υ―ΉΒέΙ άο―ΑΗυΫΎΓ±Θ§Ρ≥ΙΛ≥ßΫ”ΒΫ“Μ≈ζΦΆΡνΤΖ…ζ≤ζΕ©ΒΞΘ§Α¥“Σ«σ‘Ύ15ΧλΡΎΆξ≥…Θ§‘ΦΕ®’β≈ζΦΆΡνΤΖΒΡ≥ω≥ßΦέΈΣΟΩΦΰ20‘ΣΘ§…ηΒΎxΧλΘ®1ΓήxΓή15Θ§«“xΈΣ’ϊ ΐΘ©ΟΩΦΰ≤ζΤΖΒΡ≥…±Ψ «p‘ΣΘ§p”κx÷°ΦδΖϊΚœ“Μ¥ΈΚ· ΐΙΊœΒΘ§≤ΩΖ÷ ΐΨί»γ±μΘΚ
Χλ ΐΘ®xΘ© | 1 | 3 | 6 | 10 |
ΟΩΦΰ≥…±ΨpΘ®‘ΣΘ© | 7.5 | 8.5 | 10 | 12 |
»ΈΈώΆξ≥…ΚσΘ§Ά≥ΦΤΖΔœ÷ΙΛ»Υάν ΠΗΒΒΎxΧλ…ζ≤ζΒΡ≤ζΤΖΦΰ ΐyΘ®ΦΰΘ©”κxΘ®ΧλΘ©¬ζΉψ»γœ¬ΙΊœΒΘΚy=![]() Θ§
Θ§
…ηάν ΠΗΒΒΎxΧλ¥¥‘λΒΡ≤ζΤΖάϊ»σΈΣW‘ΣΘ°
Θ®1Θ©÷±Ϋ”–¥≥ωp”κxΘ§W”κx÷°ΦδΒΡΚ· ΐΙΊœΒ ΫΘ§≤ΔΉΔΟςΉ‘±δΝΩxΒΡ»Γ÷ΒΖΕΈßΘΚ
Θ®2Θ©«σάν ΠΗΒΒΎΦΗΧλ¥¥‘λΒΡάϊ»σΉν¥σΘΩΉν¥σάϊ»σ «Εύ…Ό‘ΣΘΩ
Θ®3Θ©»ΈΈώΆξ≥…ΚσΘ°Ά≥ΦΤΖΔœ÷ΤΫΨυΟΩΗωΙΛ»ΥΟΩΧλ¥¥‘λΒΡάϊ»σΈΣ299‘ΣΘ°ΙΛ≥ß÷ΤΕ®»γœ¬Ϋ±άχ÷ΤΕ»ΘΚ»γΙϊ“ΜΗωΙΛ»ΥΡ≥Χλ¥¥‘λΒΡάϊ»σ≥§ΙΐΗΟΤΫΨυ÷ΒΘ§‘ρΗΟΙΛ»ΥΒ±ΧλΩ…ΜώΒΟ20‘ΣΫ±ΫπΘ°«κΦΤΥψάν ΠΗΒΙ≤Ω…ΜώΒΟΕύ…Ό‘ΣΫ±ΫπΘΩ