题目内容
一条抛物线y=2（x-2）2+k的顶点A在直线y=2x-3上，求顶点A的坐标．
考点：二次函数的性质
专题：
分析：根据顶点式解析式写出顶点坐标，然后代入直线解析式计算即可得解．
解答：解：抛物线y=2（x-2）2+k的顶点A的坐标为（2，k），
代入直线y=2x-3得，2×2-3=k，
解得k=1．
所以顶点A的坐标为（2，1）．
代入直线y=2x-3得，2×2-3=k，
解得k=1．
所以顶点A的坐标为（2，1）．
点评：本题考查了二次函数的性质，一次函数图象上点的坐标特征，熟练掌握利用顶点式解析式写出顶点坐标的方法是解题的关键．
练习册系列答案
导学全程练创优训练系列答案
相关题目
两个相似多边形的面积比是9：16，其中较小多边形的周长为36cm，则较大多边形的周长为（ ）
| A、48cm | B、54cm |
| C、56cm | D、64cm |
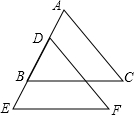如图：AC∥DF，AD=BE，BC∥EF．求证：△ABC≌△DEF．