题目内容
已知:如图,在矩形ABCD中,AB=10,BC=12,四边形EFGH的三个顶点E、F、H分别在矩形ABCD的边AB、BC、DA上,AE=2.
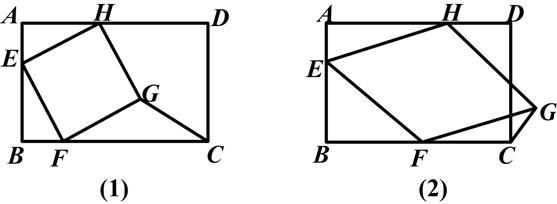
(1)如图(1),当四边形EFGH为正方形时,求△GFC的面积.
(2)如图(2),当四边形EFGH为菱形,且BF=a时,求△GFC的面积(用含a的代数式表示).
(3)在(2)的条件下,△GFC的面积能否等于2?请说明理由.
(1)10 (2)12-a (3)不能
【解析】
解:(1)过点G作GM⊥BC于M.
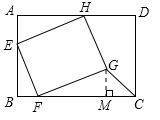
在正方形EFGH中,
∠HEF=90°,EH=EF,
∴∠AEH+∠BEF=90°.
∵∠AEH+∠AHE=90°,
∴∠AHE=∠BEF.
又∵∠A=∠B=90°,
∴△AHE≌△BEF.
同理可证△MFG≌△BEF.
∴GM=BF=AE=2.∴FC=BC-BF=10.
∴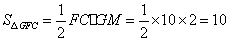 .
.
(2)过点G作GM⊥BC交BC的延长线于M,连接HF.
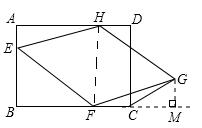
∵AD∥BC,∴∠AHF=∠MFH.
∵EH∥FG,∴∠EHF=∠GFH.
∴∠AHE=∠MFG.
又∵∠A=∠GMF=90°,EH=GF,
∴△AHE≌△MFG.∴GM=AE=2.
∴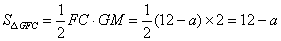 .
.
(3)△GFC的面积不能等于2.
说明:∵若S△GFC=2,则12-a=2,∴a=10.
此时,在△BEF中,
 .
.
在△AHE中,
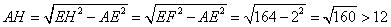 ,
,
∴AH>AD,即点H已经不在边AD上,故不可能有S△GFC=2.
【难度】困难

 阅读快车系列答案
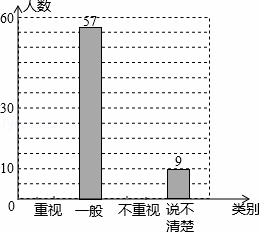
阅读快车系列答案某教研机构为了了解在校初中生阅读数学教科书的现状,随机抽取某校部分初中学生进行了调查,依据相关数据绘制成以下不完整的统计表,请根据图表中的信息解答下列问题:
某校初中生阅读数学教科书情况统计图表
类别 | 人数 | 占总人数比例 |
重视 | a | 0.3 |
一般 | 57 | 0.38 |
不重视 | b | c |
说不清楚 | 9 | 0.06 |
(1)求样本容量及表格中a,b,c的值,并补全统计图;
(2)若该校共有初中生2300名,请估计该校“不重视阅读数学教科书”的初中人数;
(3)①根据上面的统计结果,谈谈你对该校初中生阅读数学教科书的现状的看法及建议;
②如果要了解全省初中生阅读数学教科书的情况,你认为应该如何进行抽样?
 并写出它的非负整数解.
并写出它的非负整数解.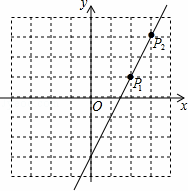


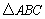 中,AB=AC,∠ABC =
中,AB=AC,∠ABC =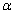 ,D是BC边上一点,以AD为边作
,D是BC边上一点,以AD为边作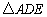 ,使AE=AD,
,使AE=AD,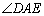 +
+ =180°.
=180°.
 ,并将不等式组的解集在所给数轴上表示出来.
,并将不等式组的解集在所给数轴上表示出来.