题目内容
如图,在平行四边形ABCD中,点E是边AD的中点,BE的延长线与CD的延长线相交于点F.
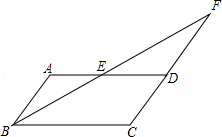
(1)求证:△ABE≌△DFE;
(2)试连接BD、AF,判断四边形ABDF的形状,并证明你的结论.
(1)证明:∵四边形ABCD是平行四边形,∴AB∥CF,∴∠1=∠2,∠3=∠4,
∵E是AD的中点,∴AE=DE,∴△ABE≌△DFE;
(2)四边形ABDF是平行四边形.理由如下:
∵△ABE≌△DFE,∴AB=DF,又∵AB∥DF,∴四边形ABDF是平行四边形.
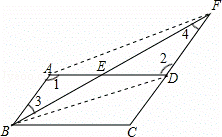
【解析】
分析:(1)用ASA证明△ABE≌△DFE;
(2)四边形ABDF是平行四边形,可用对角线互相平分的四边形是平行四边形来证明.
解:(1)∵四边形ABCD是平行四边形,∴AB∥CF,∴∠1=∠2,∠3=∠4,
∵E是AD的中点,∴AE=DE,∴△ABE≌△DFE;
(2)四边形ABDF是平行四边形.理由如下:
∵△ABE≌△DFE,∴AB=DF,又∵AB∥DF,∴四边形ABDF是平行四边形.

【难度】一般

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
 的图象在第二、四象限,那么
的图象在第二、四象限,那么 的取值范围是 .
的取值范围是 . 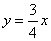 与一次函数
与一次函数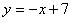 的图像交于点A.
的图像交于点A.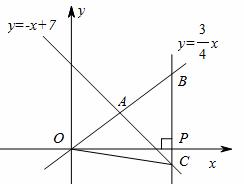

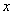 轴上一点P(
轴上一点P(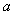 ,0),过点P作
,0),过点P作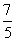 OA,求△OBC的面积.
OA,求△OBC的面积.

 四边形是菱形,则称原平行四边形为n阶准菱形.如图1,▱ABCD中,若AB=1,BC=2,则▱ABCD为1阶准菱形.
四边形是菱形,则称原平行四边形为n阶准菱形.如图1,▱ABCD中,若AB=1,BC=2,则▱ABCD为1阶准菱形.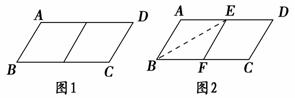

 ;
;
 .
.