题目内容
2．下列等式从左到右的变形中，属于因式分解的是（ ）| A． | x+1=x（1+$\frac{1}{x}$） | B． | x2-4+4x=（x+2）（x-2）+4x | ||
| C． | （x+3）（x-3）=x2-9 | D． | x2-2x-3=（x-3）（x+1） |
分析 根据因式分解的意义，可得答案，
解答 解：A、没把多项式转化成几个整式积的形式，故A不符合题意；
B、没把多项式转化成几个整式积的形式，故B不符合题意；
C、是整式的乘法，故C不符合题意；
D、把多项式转化成几个整式积的形式，故D符合题意；
故选：D．
点评 本题考查了因式分解的意义，利用因式分解的意义是解题关键．
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
13．
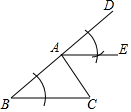如图，△ABC中，AB＞AC，∠CAD为△ABC的外角，观察图中尺规作图的痕迹，则下列结论错误的是（ ）
如图，△ABC中，AB＞AC，∠CAD为△ABC的外角，观察图中尺规作图的痕迹，则下列结论错误的是（ ）| A． | ∠DAE=∠B | B． | ∠EAC=∠C | C． | AE∥BC | D． | ∠DAE=∠EAC |
10．下列命题中，是真命题的是（ ）
| A． | 相等的角是对顶角 | |
| B． | 和为180°的两个角是邻补角 | |
| C． | 两条直线被第三条直线所截，同位角相等 | |
| D． | 过直线外一点，有且只有一条直线与已知直线平行 |
7．植树节这天，35名同学共栽了90棵树苗，其中男生每人栽3棵，女生每人栽2棵．若设男生有x人，女生有y人，则下列方程组正确的是（ ）
| A． | $\left\{\begin{array}{l}{x+y=35}\\{2x+3y=90}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{x+y=35}\\{3x+2y=90}\end{array}\right.$ | C． | $\left\{\begin{array}{l}{x+y=90}\\{2x+3y=35}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{x+y=90}\\{3x+2y=35}\end{array}\right.$ |
14．能说明“对于任何实数a，|a|＞-a”是假命题的一个反例可以是（ ）
| A． | a=-2-1 | B． | a=$\frac{1}{3}$ | C． | a=1-3 | D． | a=π |
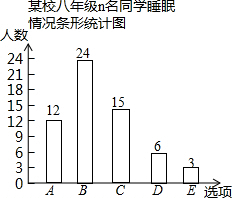某校八年级学生会为了解本年级600名学生的睡眠情况，将同学们某天的睡眠时长t（小时）分为A，B，C，D，E（A：9≤t≤24；B：8≤t＜9；C：7≤t＜8；D：6≤t＜7；E：0≤t＜6）五个选项，进行了一次问卷调查，随机抽取n名同学的调查问卷并进行了整理，绘制成如下条形统计图，根据统计图提供的信息解答下列问题：