Question

【题目】在平面直角坐标系中，直线与轴交于点，与轴交于点，抛物线经过点．

（1）求满足的关系式及的值；

（2）当时，求抛物线解析式，并直接写出当时的取值范围．

（3）当时，若的函数值随的增大而增大，求的取值范围；

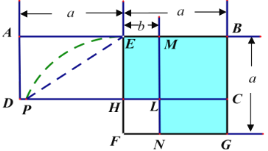
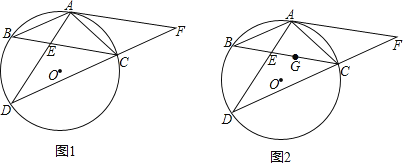
（4）如图，当时，在第二象限的抛物线上找点，使的面积最大，求出点坐标．

Answer 1

【答案】（1）b=2a＋1，c=2；（2）；-2＜x＜3；（3）；（4）（-1,2）

【解析】

（1）先求出点A和点B的坐标，然后将点A和点B的坐标代入二次函数解析式中即可求出结论；

（2）联立方程即可求出a和b的值，从而求出抛物线的解析式，然后求出抛物线的对称轴，即可求出抛物线与x轴的另一个交点坐标，最后根据图象即可求出结论；

（3）用含a的式子表示出抛物线的对称轴，然后根据抛物线对称轴两侧的增减性即可求出结论；

（4）先求出抛物线的解析式，过点P作PQ⊥x轴交AB于点Q，设点P的坐标为（x，），则点Q的坐标为（x，），从而求出PQ，然后利用“铅垂高，水平宽”即可求出S△PAB与x的函数关系式，然后利用二次函数求最值即可求出结论．

解：（1）将y=0代入中，解得：x=-2；将x=0代入中，解得：y=2

∴点A的坐标为（-2,0），点B的坐标为（0,2）

将点A、B的坐标代入中，得

解得：b=2a＋1，c=2；

（2）∵

解得：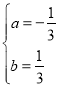

∴抛物线解析式为

抛物线的对称轴为：直线x==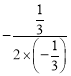

∴抛物线与x轴的另一个交点坐标为×2－（-2）=3

由图象可知：当时，-2＜x＜3

（3）抛物线的对称轴为直线x=，开口向下

∴x≤时，y随x的增大而增大

∵当时，若的函数值随的增大而增大，

∴≥0

∴2a＋1≥0

解得：a≥

∴

（4）当时，抛物线的解析式为

过点P作PQ⊥x轴交AB于点Q

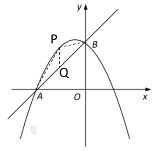
设点P的坐标为（x，），则点Q的坐标为（x，）

∴PQ=（）－（）=

∴S△PAB=PQ·

=（）×2

=

=

∴当x=-1，S△PAB最大，S△PAB最大值为1

此时点P的坐标为（-1,2）